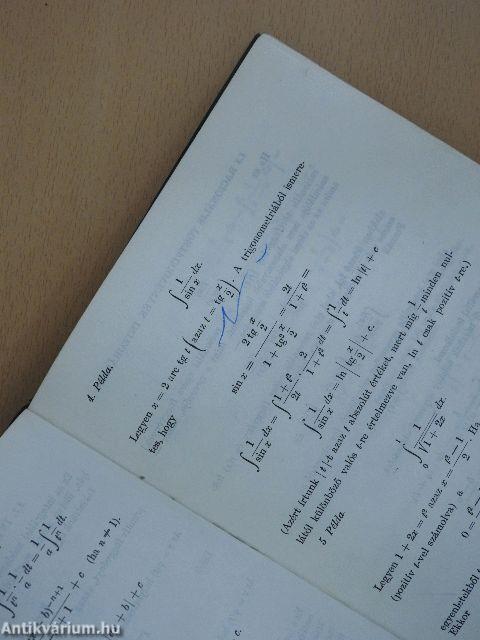| Kiadó: | Közgazdasági és Jogi Könyvkiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött keménykötés |
| Oldalszám: | 510 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 20 cm x 14 cm |
| ISBN: | |
| Megjegyzés: | Fekete-fehér ábrákat tartalmaz. |
| Előszó | 9 |
| Halmazok, leképezések, függvények | 11 |
| Halmazok, halmazok számossága | 11 |
| Függvények, operációk | 21 |
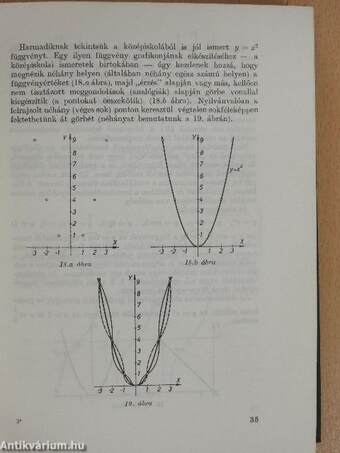
| Függvények grafikonja, alapfüggvények | 33 |
| Paraméteres alakban megadott függvények | 43 |
| A határérték | 45 |
| Környezet. Torlódási hely. Számsorozat | 45 |
| Összehúzódó zárt intervallumok elve | 50 |
| A határérték fogalma | 53 |
| A határérték-tulajdonságok | 56 |
| Példák sorozatokra | 62 |
| Folytonos és szakadásos függvények | 69 |
| Függvények határértéke | 69 |
| Példák folytonos függvényekre | 73 |
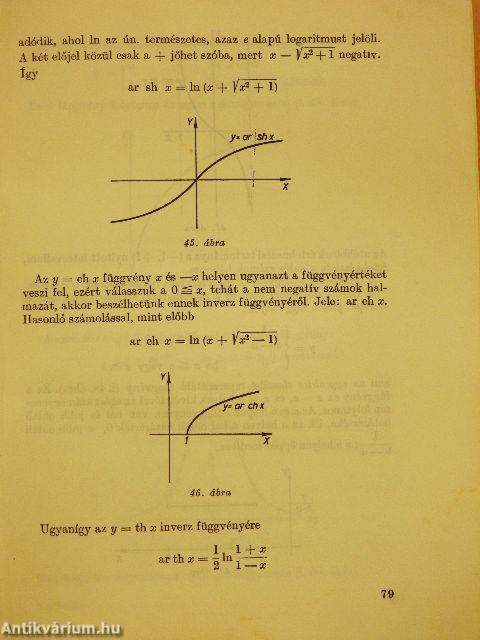
| A gyakorlatban előforduló néhány fontosabb függvény | 75 |
| Folytonos függvények alaptulajdonságai | 77 |
| Differenciálhányados, derivált függvény, deriválási szabályok, elaszticitás | 85 |
| A differnciálhányados fogalma | 85 |
| A különbségi hányados és differenciálhányados geometriai és mechanikai jelentése | 87 |
| A derivált függvény | 89 |
| Az alapfüggvények derivált függvénye | 94 |
| Magasabbrendű deriváltak | 103 |
| A függvény elaszticitása | 104 |
| A differenciálszámítás alaptételei, függvények vizsgálata | 109 |
| Függvények növekedése és csökkenése | 109 |
| Helyi szélső értékek | 114 |
| Konvex és konkáv függvények, inflexiós pont | 119 |
| Taylor sor, egyenletek valós gyökei | 134 |
| Taylor-polinom, Taylor-sor maradéktagja, maclaurin-sor | 134 |
| Taylor-sor felhasználása, helyi szélső értékek meghatározása | 142 |
| A Taylor-polinom algebrai vonatkozásai | 145 |
| Egyenletek valós gyökeinek közelítő meghatározása | 148 |
| Végtelen sorok | 152 |
| A függvényvizsgálat alkalmazásai | 163 |
| Maximum-minimum feladatok | 163 |
| Költségfüggvény | 176 |
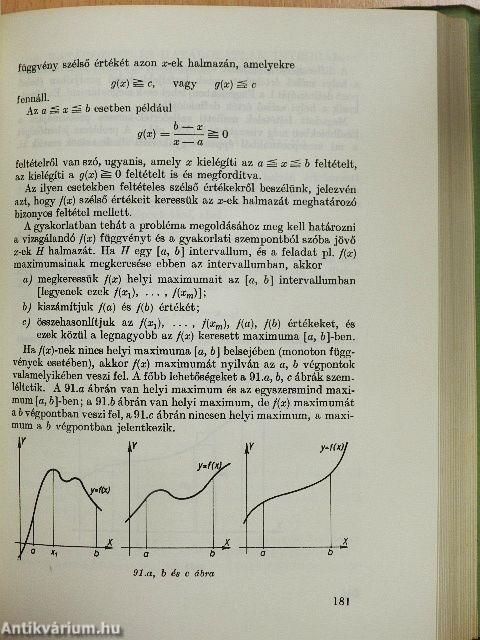
| Megjegyzések a maximum-minimum számításához | 180 |
| Határozott és határozatlan integrál | 183 |
| A határozott integrál fogalma | 183 |
| Határozott integrál fontosabb tulajdonságai | 190 |
| A határozatlan integrál | 194 |
| A Leibnitz-Newton-féle képlet | 197 |
| A parciális integrálás módszere | 199 |
| A Wallis-formula | 204 |
| Integrálás helyettesítéssel | 207 |
| Racionális törtfüggények integrálása | 210 |
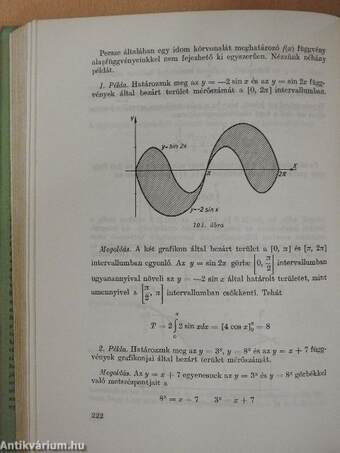
| Az integrálszámítás néhány alkalmazása | 220 |
| A határozott integrál közelítő kiszámítása | 238 |
| Improprius integrálok | 246 |
| Néhány speciális improprius integrál | 252 |
| A Stirling-formula | 262 |
| Fourier-sorok | 265 |
| Többváltozós függvények | 284 |
| A többváltozós függvény fogalma | 284 |
| Többváltozós függvény határértéke, folytonossága | 292 |
| A parciális differenciálhányados | 293 |
| A totális differenciálhányados | 296 |
| Irány menti differenciálhányados | 297 |
| A közvetett függvény parciális differenciálhányadosa | 299 |
| Implicit függvény deriválása | 300 |
| Magasabbrendű parciális deriváltak | 301 |
| Taylor-formula | 306 |
| Szélső értékek | 310 |
| Feltételes szélsőérték | 320 |
| A Lagrange-féle multiplikátor-módszer | 325 |
| A Kuhn-Tucker-féle tétel | 331 |
| Közgazdasági alkalmazások | 340 |
| Többszörös integrálok | 350 |
| A többszörös integrál fogalma | 350 |
| Többszörös integrál transzformációja | 362 |
| Improprius többszörös integrál | 369 |
| Több változós függvény Stieltjes-integrálja | 373 |
| Paraméteres integrál | 378 |
| Komplex változós függvény | 381 |
| A komplex változós függvény fogalma | 381 |
| Komplex számsorozatok, a komplex változós függvény folytonossága | 383 |
| Hatványsorok | 384 |
| Hatványsorral értelmezett komplex változós függvények | 389 |
| Komplex változós függvény differenciálhányadosa | 392 |
| Hatványsor deriváltja | 396 |
| Komplex változós függvény határozott integrálja | 399 |
| Mátrixok halmazán értelmezett függvények | 403 |
| A függvény értelmezése, torlódási hely, határérték | 403 |
| Mátrix-hatványsor | 404 |
| Absztrakt halmazon értelmezett függvények | 412 |
| Differenciálegyenletek | 418 |
| A közönséges differenciálegyenlet fogalma | 418 |
| Változók szétválasztásával megoldható differenciál-egyenlet | 419 |
| Homogén differenciálegyenlet | 422 |
| Homogénre visszavezethető differenciálegyenletek | 425 |
| Lineáris differenciálegyenlet | 426 |
| Elsőrendű lineáris differenciálegyenlet állandó együtthatókkal | 429 |
| Inhomogén lineáris differenciálegyenlet állandó együtthatókkal | 432 |
| Inhomogén lineáris differenciálegyenlet | 438 |
| Kezdeti feltételek | 442 |
| Differenciálegyenlet-rendszer | 443 |
| Parciális differenciálegyenlet | 448 |
| Differenciálegyenletek | 455 |
| Differenciálegyenletekről általában | 455 |
| Differenciálegyenlet diszkrét és folytonos megoldása | 457 |
| Elsőrendű lineáris differenciálegyenlet | 460 |
| n-edrendű lineáris differenciálegyenlet | 461 |
| Néhány kiegészíté | 466 |
| Differenciál | 466 |
| Konves halmazok az En térben | 468 |
| A Brouwer-féle fixponttétel és Kakutanitól származó általánosítása | 472 |
| Feladatok | 478 |
| Függelék | 493 |
| A matematikai analízis történetéből | 493 |
| A modell és az objektív valóság | 496 |
| Nevesebb külföldi és magyar matematikusok és közgazdász-matematikusok | 501 |
| Felhasznált irodalom | 505 |
| Tárgymutató | 507 |
A védőborító széle szakadt, a lapélek foltosak. A címlapon tulajdonosi bejegyzés található.
Könyvtári könyv volt. A lapélek és néhány lap foltos. Néhány lapon jelölések láthatók.
Védőborító nélküli példány.
A védőborító elszíneződött.
Folytatás Microsoft-tal