1.117.824
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Bevezetés az elméleti fizikába 1-2.
| Kiadó: | Akadémiai Kiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött keménykötés |
| Oldalszám: | 1.271 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 25 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Fekete-fehér ábrákkal. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| I. kötet | |
| Előszó | 17 |
| Bevezetés | 19 |
| Mechanika | |
| Bevezetés | 23 |
| Az anyagi pont mechanikája | |
| A vektortan alapjai | 26 |
| A tömegpont kinematikája | 36 |
| A mechanika alaptörvényei. Newton axiómái | 42 |
| Mozgásegyenletek | 45 |
| az erő idő és pálya szerinti integrálja. A munka | 46 |
| A potenciál és az energiatétel | 49 |
| Az erő momentuma és az impulzusmomentum közötti összefüggés | 55 |
| Rugalmas erők. Egyszerű harmonikus mozgás | 56 |
| A csillapított harmonikus mozgás | 61 |
| A centárlis mozgás | 65 |
| A Kepler-probléma | 67 |
| A Newton-féle tömegvonzási törvény. Gravitációs erők | 71 |
| A mesterséges holdak mozgása. Első és második kozmikus sebesség | 73 |
| A bolygók mozgása | 76 |
| Rakétamozgás. A Ciolkovszkij-egyenlet | 78 |
| A kényszernek alávetett tömegpont mechanikája. Kényszererők | 79 |
| A lejtőn való mozgás | 81 |
| A matematikai síkinga | 83 |
| a mozgásegyenletek mozgó koordinátarendszerben | 89 |
| Pontrendszerek mechanikája | |
| A tömegközéppont tétele | 97 |
| Folytonos eloszlású rendszerek tömegközéppontja | 100 |
| Az impulzusmomentum tétele | 101 |
| Pontrendszerek összenergiája | 103 |
| A mozgásegyenletek 10 integrálja | 105 |
| Az anyag korpuszkuláris elmélete | |
| Bevezetés | 13 |
| A korpuszkulák létezésének kimutatásai. Kémiai alaptörvények | 14 |
| Az elektrolízis Faraday-féle törvényei | 16 |
| A Brown-féle mozgás | 16 |
| Töltéssel bíró sugarak részeinek megszámlálása. Wilson kísérlete, szcintilláció, tűszámláló, héliumrészek megszámlálása | 17 |
| Szilárd testek korpuszkuláris szerkezete | 19 |
| A korpuszkulák elemei sajátságai | 21 |
| Az elemi töltés meghatározása Millikan szerint | 21 |
| A töltés és a tömeg viszonyának meghatározása korpuszkulák esetében | 23 |
| Elektron, proton | 27 |
| Az Alfa-részek szóródása | 28 |
| Izotópia | 33 |
| A Franck-Hertz kísérlet. Gerjesztett atomok energianívói | 36 |
| Az atomok mágneses momentuma | 39 |
| Atomok és molekulák elektromos momentuma | 44 |
| A fotoelektromos effektus. A foton | 44 |
| A Compton-effektus | 46 |
| Anyaghullámok | 48 |
| Néhány megjegyzése az elemek periodusos rendszeréhez | 49 |
| Atommagok | 50 |
| A radioaktivitás | 62 |
| Magreakciók | 70 |
| A szilárd testek korpuszkuláris elméletének alapjai | 73 |
| A rácsenergia | 76 |
| Rácsrezgések | 83 |
| A rácsfrekvenciák meghatározása | 89 |
| A háromdimenziós rácsok rezgései | 103 |
| A mechanika elvei | |
| Az egyensúly és mozgás feltételei | 106 |
| Néhány egyszerű fogalom a variációszámítás köréből | 113 |
| A Virtuális munka elve, mint variációs elv | 115 |
| Az egyensúly stabilitásának feltétele | 115 |
| A Hamilton-féle elv | 116 |
| Általános koordináták | 120 |
| Holonom és nem holonom kényszerek | 122 |
| A Lagrange-féle másodfajú egyenletek | 123 |
| A Hamilton-féle kanonikus egyenletek | 128 |
| A legkisebb hatás elve | 133 |
| Kanonikus transzformáció | 138 |
| Ciklikus változók. A Hamilton-Jacobi féle differenciaegyenlet | 142 |
| Merev test mechanikája | |
| A merev test kinematikája | 148 |
| A merev test mozgásegyenletei | 164 |
| Merev test forgása egy rögzített tengely körül | 164 |
| Párhuzamos tengelyekre vonatkozó tehetetlenségi momentumok közti összefüggés | 168 |
| Rögzített tengely körül forgó merev test kinetikus energiája | 170 |
| A tehetetlenségi momentum függése a forgástengely irányításától | 172 |
| A tehetetlenségi ellipszoid | 173 |
| Folytonos anyageloszlású testek tehetetlenségi és deviációs momentumai | 175 |
| Tetszőleges tengelyre vonatkozó tehetetlenségi momentumok meghatározása | 176 |
| A merev test egy rögzített pontja körüli mozgása. Az Euter-féle egyenletek | 176 |
| A merev test pontkörüli mozgásának tárgyalása az Euler-féle egyenletek alapján, ha a külső erők momentuma eltűnik | 180 |
| Az Euler-féle egyenletek integrálása, ha a külső erők momentuma eltűnik | 183 |
| Az Euler-féle szögeknek mint az idő függvényeinek meghatározása, ha a külső erők momentuma eltűnik | 192 |
| A merev test mozgása egy rögzített pontja körül, ha rá külső erő forgatómomentumot gyakorol | 194 |
| A merev test sztatikájának alapfogalmai | 198 |
| Deformálható testek mechanikája | |
| Bevezetés | 203 |
| Lineáris transzformációk | 203 |
| A deformálható testek kinematikája | 221 |
| A deformálható testek dinamikája | 229 |
| A rugalmas testek mechanikája | 241 |
| Síkhullámok izotróp rugalmas közegben | 252 |
| Cseppfolyós és légnemű testek | 269 |
| Cseppfolyós és légnemű testek egyensúlya | 270 |
| Cseppfolyós és lgnemű testek mozgása | 274 |
| A Bernoulli-féle egyenlet | 279 |
| Örvénymentes áramlások | 281 |
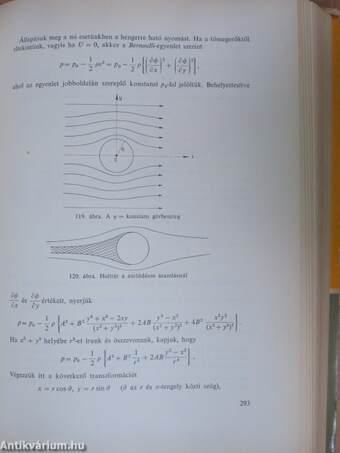
| Stacionárius, örvénymentes síkáramlás | 283 |
| Relativitáselmélet | |
| A Galile-féle relativitási elv | 301 |
| Az Einstein-féle relativitási elv | 303 |
| A Michelson-Morley kísérlet | 306 |
| A Lorentz-transzformáció | 308 |
| Relativisztikus kinematika | 311 |
| Relativisztikus mozgásegyenletek | 320 |
| Rakétamozgás | 322 |
| Erők transzformációja | 324 |
| A relativisztikus energia | 325 |
| Négyesvektorok | 329 |
| Az általános relativitás elmélet alapja | 339 |
| Elektrodinamika | |
| Bevezetés | 343 |
| Vektoranalízis | |
| Vektormezők, skaláris mezők | 344 |
| Gradiens, potenciál | 345 |
| Trajektóriák | 346 |
| Ekvipotenciális felületek | 346 |
| Vonalintegrál | 347 |
| Felületi integrál | 349 |
| Divergencia | 350 |
| Gauss tétele | 352 |
| Green tétele | 352 |
| Stokes tétele | 354 |
| A rotáció | 357 |
| Felületes divergencia és felületi rotáció | 361 |
| Az elektrosztatikus tér | |
| Az elektromos térerősség és elektromos töltés | 364 |
| Az elektromos töltés mint az erőfluxus forrása | 365 |
| Mértékrendszerek | 368 |
| Az elektrosztatikus terek jellemző tulajdonságai | 368 |
| Az elektromosság elhelyezkedése vezetőkön | 370 |
| Az elektrosztatika alapproblémája | 371 |
| A pontszerű töltés potenciálja | 372 |
| Különböző töltésrendszerek potenciálja | 374 |
| Vezetők a térben. Gömbkondenzátor | 381 |
| Az elektrosztatikus tér szigetelőkben. Dielektromos közegek | 382 |
| Dielektrikumok polarizációja | 386 |
| Az elektrosztatikus tér energiája | 390 |
| Anizotrop dielektrikumok | 395 |
| Stacionárius áramok | |
| Definíciók | 397 |
| Ohm törvénye | 397 |
| Joule törvénye | 402 |
| Kirchhoff törvényei | 403 |
| A magnetosztatikus tér | |
| Mágneses alapjelenségek és a mágnesség alaptörvényei | 406 |
| Permanens mágnes mágneses tere | 410 |
| Elektromos áram mágneses tere | 411 |
| Zárt lineáris áram és a rajta átfektetett mágneses dipolréteg ekvivalenciája | 415 |
| Áramok mágneses terének meghatározása, ha a környzeő közegben | 420 |
| Az időben lassan változó kvázistacionárius terek | |
| Bevezetés | 423 |
| Az indukciós törvénye. Az elektromágneses tér második alapegyenlete | 423 |
| Kölcsönös indukció | 425 |
| Önindukció | 426 |
| Egymással össze nem függő n lineáris áramkör mágneses energiája | 430 |
| Váltóáramú körök | 431 |
| Gyorsan váltakozó elektromágneses terek | 439 |
| Az elektromágneses tér első alapegyenletei | 441 |
| Az elektromágneses tér alapegyenletei | 443 |
| A sugárvektor | |
| Elektromágneses hullámok | |
| Elektromágneses síkhullámok dielektrikumokban | 445 |
| elliptikusan, cirkulárisan és lineárisan poláros hullámok | 452 |
| Síkhullámok vezető közegben | 457 |
| Síkhullámok visszaverődése és törése | 459 |
| A teljes visszaverődés | 469 |
| Síkhullámok összetétele | 472 |
| Állóhullámok | 474 |
| A hullámcsoport. Csoportsebesség | 475 |
| Gömbhullámok | 478 |
| A Huyghens-féle elv. Kirchhoff formulája | 493 |
| Az elhajlásjelenségek felosztása | 498 |
| Egyszerű harmonikus rezgések összetétele a komplex számsíkon | 502 |
| Fraunhofer-féle elhajlásjelenségek egyszerű résen, vonalas, kereszt- és térbeli rácson | 504 |
| Az elektrodinamika alapegyenleteinek egységes levezetése és az ezekből levont általános következtetések | |
| Maxwell-féle egyenletek és a határfeltételek egységes származtatása | 517 |
| Elektromágneses jelenségek osztályozása és egyes speciális terek alapegyenleteinek levezetése az általános alapegyenletekből | 519 |
| Elektromágneses potenciálok | 521 |
| Retardált potenciálok | 525 |
| A Maxwell-féle feszültségek | 528 |
| Elektromágneses impulzus | 531 |
| A sugárzás nyomása | 532 |
| A harmadik axióma az elektromágneses térben | 534 |
| Relativisztikus elektrodinamika | |
| Az elektrodinamika alapegyenleteinek Lorentz-invarianciája | 535 |
| Az elektromos töltés és az elektromágneses térerősségek transzformációs szabályai | 539 |
| Négyestenzorok | 543 |
| Doppler-effektus és aberráció | 554 |
| Termodinamika | |
| Bevezetés | 559 |
| A termodinamika főtételei | |
| A hőmérséklet fogalma és a hőmérsékleti skála | 591 |
| Termodinamikai rendszerek. Állapotjelzők és állapotfüggvények | 563 |
| Az ideális gáz állapotegyenlete | 567 |
| A termodinamika első főtétele | 569 |
| Hőkapacitás | 573 |
| Adiabatikus folyamatok | 576 |
| A termodinamika második főtétele | 577 |
| A Carnot-féle körfolyamat | 578 |
| Az entrópia | 587 |
| A második főtétel matematikai megfogalmazása | 590 |
| A termodinamika harmadik főtétele | 592 |
| Az állapotegyenletek integrálhatósága | |
| Az állapotegyenletek integrálhatóságának feltétele. Az entrópia meghatározása | 594 |
| Az ideális gáz entrópiája | 596 |
| A van der Waals-féle állapotegyenlet | 599 |
| Kondenzáció | 602 |
| Mágneses anyagok termikus viselkedése | 605 |
| A szupravezető átmenet termodinamikája | 610 |
| Termodinamikai egyensúly | |
| Az egyensúly feltételei | 615 |
| Homogén rendszerek | 617 |
| Az ideális gáz termodinamikája | 624 |
| Kémiai folyamatok és kémiai egyensúly | 632 |
| Heterogén rendszerek | 636 |
| A Clausius-Clapeyron egyenlet | 340 |
| II. kötet | |
| Az anyag korpuszkuláris elmélete statisztikus mechanika | |
| Előszó és bevezetés | 11 |
| Az anyag korpuszkuláris elmélete | |
| Bevezetés | 13 |
| A korpuszkulák létezésének kimutatása. Kémiai alaptörvények | 14 |
| Az elektrolízis Faraday-féle törvényei | 16 |
| A Brown-féle mozgás | 16 |
| Töltéssel bíró sugarak részeinek megszámlálása. Wilson kísérlete, szcintilláció, tűszámláló, héliumrészek megszámlálása | 17 |
| Szilárd testek korpuszkuláris szerkezete | 19 |
| A korpuszkulás elemi sajátságai | 21 |
| Az elemi töltés meghatározása Millikan szerint | 21 |
| A töltés és a tömeg viszonyának meghatározása korpuszkulás esetében | 23 |
| Elektron, proton | 27 |
| Az Alfa-részek szóródása | 28 |
| Izotópia | 33 |
| A Franck-Hertz kísérlet. Gerjesztett atomok energianívói | 36 |
| Az atomok mágneses momentuma | 39 |
| Atomok és molekulák elektromos momentuma | 44 |
| A fotoelektromos effektus. A foton | 44 |
| A Compton-effektus | 46 |
| Anyaghullámok | 48 |
| Néhány megjegyzés az elemek periódusos rendszeréhez | 49 |
| Atommagok | 50 |
| A radioaktivitás | 62 |
| Magreakciók | 70 |
| A szilárd testek korpuszkuláris elméletének alapjai | 73 |
| A rácsenergia | 76 |
| Rácsrezgések | 83 |
| A rácsefrekvenciák meghatározása | 89 |
| A háromdimenziós rácsok rezgései | 103 |
| Longitudinális és tranverzális rácsrezgések | 110 |
| Gázok diffúziója | 119 |
| Töltött részek áramlása külső erőtér hatására gázban | 129 |
| Statisztikus mechanika | |
| Bevezetés | 132 |
| A gázok korpuszkuláris szerkezete | 132 |
| Entrópia és valószínűség | 133 |
| Ideális gáz sűrűségeloszlásának meghatározása. A klasszikus vagy Boltzmann-féle statisztika | 136 |
| Liouville tétele. A fázistér. | 140 |
| A Maxwell-Boltzmann-féle energiaeloszlás | 141 |
| Sebességeloszlás ideális gázban | 144 |
| Ideális gáz állapotegyenlete. A Boltzmann-állandó és gázállandó közti összefüggés | 148 |
| Az ekvipartició tétele és alkalmazása a fajhőre | 149 |
| A kvantumstatisztika alapjai | 152 |
| A Bose-Einstein statisztika | 153 |
| Az egyatomos Bose-gáz | 157 |
| Az ideálils gáz elfajulása alacsony hőmérsékleten | 162 |
| A plazma | 166 |
| A hőmérsékleti sugárzás | 170 |
| Anyag és sugárzás hőmérsékleti egyensúlya | 176 |
| A Fermi-Dirac-statisztika | 178 |
| Az elektrongáz | 182 |
| Az elektrongáz viselkedése extrém körülmények között | 185 |
| Az elektrongáz fajhője | 193 |
| A relativisztikusan elfajult elektrongáz | 194 |
| A szilárd testek fajhője | 198 |
| Kvantummechanika | |
| A Bohr-féle atomelmélet | |
| A hidrogénatom Bohr-féle elmélete | 205 |
| A Moseley-törvény | 211 |
| Alkáli- és hasonló atomok spektrumai | 212 |
| A korrespondencia-elv | 214 |
| A Stark- és Zeeman-effektus | 215 |
| Spinkvantumszám, belső kvantumszám | 216 |
| A hiperfinom struktúra | 217 |
| A többelektronkonfigurációk energiatermjei és azok szimbólumai | 218 |
| Pauli elv. A periódusos rendszer felépítése a Pauli-elv alapján | 219 |
| Az elemek kémiai viselkedésének értelmezése az atomszerkezet alapján. Néhány megjegyzés a kémiai kötésre vonatkozóan | 222 |
| A sávos spektrumok elemeinek rövid összefoglalása | 223 |
| A hullámmechanika alapjai | |
| Általános áttekintés | 226 |
| A Heisenberg-féle határozatlansági reláció | 227 |
| A kauzalitás elve a kvantummechanikában | 231 |
| Hullámok fázis- és csoportsebessége | 232 |
| Anyaghullámok | 234 |
| A Schrödinger-egyenlet | 238 |
| A Schrödinger-egyenlet származtatása a variációs elvből | 242 |
| Sajátfüggvények, sajátértékek | 243 |
| A klasszikus mechanika mennyiségének kvantuummechanikai értelmezése. Operátorok | 247 |
| Az elektronspin kvantumelmélete | 252 |
| A korrespondencia elv. Átmeneti valószínűségek | 258 |
| Egyszerű példák a Schrödinger-egyenlet megoldására | |
| Szabad tömegpont | 263 |
| A síkbeli rotátor | 264 |
| A harmonikus lineáris oszcillátor | 266 |
| A derékszögű potenciálvölgy | 270 |
| Részecskék áthaladása derékszögű potenciálvölgyön | 273 |
| Részecskék áthaladása a potenciálfalon. Alagúteffektus | 276 |
| Periodikus potenciál | 278 |
| Mozgás centrális erőtérben | 282 |
| Az impulzumomentum | 285 |
| A mágneses momentum | 291 |
| A háromdimenziós potenciálvölgy | 295 |
| Merev falú gömbbe zárt részecske | 296 |
| A térbeli oszcillátor | 297 |
| A hidrogénatom | 302 |
| A Kratzer-féle potenciál | 309 |
| A térbeli rotátor | 313 |
| A kéttest-probléma | 314 |
| A legegyszerűbb közelítő módszerek és alkalmazásaik | |
| Perturbációszámítás | 318 |
| Az anharmonikus lináris oszcillátor | 322 |
| Síkbeli rotátor elektromos erőtérben | 323 |
| A mag véges kiterjedésének hatása az atom energianívójára | 324 |
| A spin-pálya kölcsönhatás | 326 |
| A Zeeman-effektus kvantumelmélete | 328 |
| A hidrogénatom Stark-effektusa | 332 |
| A kételektron-probléma | 333 |
| Variációs módszer | 340 |
| A héliumatom alapállapota | 343 |
| A H2+ molekula-ion | 345 |
| Szórásszámítás | |
| A szóródás elméletének alapjai. A hatáskeresztmetszet | 350 |
| A parciális hullámok módszere | 352 |
| Szóródás háromdimenziós potenciálvölgyön | 356 |
| A szórási és kötött állapotok egységes elmélete. Szórási rezonanciák | 359 |
| A radioaktív Alfa-bomlás | 367 |
| Az integrálegyenlet-módszer | 370 |
| Szóródás merev falú gömbön | 373 |
| A Coulomb-szórás | 375 |
| Kis energiájú részecskék szóródása | 380 |
| Példák a zérus energiájú hullámfüggvény meghatározására | 385 |
| A Born-közelítés | 390 |
| Elektronok szóródása atomokon | 395 |
| Relativisztikus kvantummechanika | |
| 1/2-es spinű részecskék. A Dirac-egyenlet | 398 |
| A Dirac-egyenlet szimmetrikus alakja | 402 |
| Mozgás elektromágneses térben | 405 |
| A Dirac-egyenlet szimmetriatranszformációi | 410 |
| A szabad mozgás. Síkhullámok | 419 |
| A Dirac-egyenlet megoldása centrális erőtér esetén | 423 |
| Lineáris vektorterek a kvantumelméletben. Mátrixmechanika | |
| Bevezetés | 432 |
| Az állapotvektorok és az operátorok matematikai tulajdonságai | 433 |
| A kvantummechanika törvényeinek általános megfogalmazása | 444 |
| A mátrixmechanika alapjai | 459 |
| A lineáris harmonikus oszcillátor | 470 |
| A hullámmechanika és a mátrixmechanika kapcsolata | 474 |
| A Dirac-féle bra és két vektorok | 484 |
| Lippmann-Schwinger szóráselmélet | |
| Bevezetés | 490 |
| Kölcsönhatási reprezentáció | 490 |
| Az S operátor | 492 |
| Az átmeneti valószínűség meghatározása | 495 |
| A Lippmann-Schwinger egyenlet | 498 |
| Potenciálszórás | 499 |
| Centrális erőtér | 502 |
| Centrális szórás koordinátareprezentációban | 506 |
| A kvantummechanikai többtestprobléma | |
| A többtestprobléma Schrödinger-egyenlete | 508 |
| Az impulzusmegmaradási törvény. A súlypont mozgása | 510 |
| Az impulzusmomentum megmaradási törvénye | 515 |
| Azonos részecskék. Pauli-elv | 519 |
| Spintől független kölcsönhatás | 526 |
| Betöltési szám-reprezentáció. Emissziós és abszorpciós operátorok | 529 |
| A kölcsönhatás figyelembevétele pertubációszámítással azonos Fermi-részecskék esetén | 539 |
| A Hartree-Fock-módszer | 545 |
| A Hartree-Fock-módszer alkalmazása kételektron-problémára | 553 |
| A Hartree-Fock-módszer alkalmazása nemesgáz konfigurációjú atomokra | 560 |
| Az atomok statisztikus elmélete | 568 |
| A pszeudopotenciálok módszere | 572 |
| Térelméleti módszerek alkalmazása a kvantummechanikai többtest problémában | |
| Bevezetés | 576 |
| A Green-függvényes eljárás | 578 |
| Gráftechnika | 580 |
| A széteső gráfok | 587 |
| Az alapállapot-gráfok és a linked-cluster formula | 591 |
| Az alapállapot energiája és a sajátfüggvénye | 592 |
| Kvázirészecske gerjesztések | 595 |
| Diagonális gráfok és a független kvázirészecske közelítés | 597 |
| Perturbációszámítás | 599 |
| A Bethe-Goldstone-féle módszer | 602 |
| A Bruekckner-módszer | 606 |
| Fermi-gázok és folyadékok | 611 |
| Fermi-folyadékok alapállapota | 614 |
| Kvázirészecske gerjesztés Fermi-folyadékban | 617 |
| Az egyes közelítő módszerek alkalmazási köre, kis és nagy sűrűségű határeset | 621 |
| Ajánlott irodalom | 623 |
| Név- és tárgymutató | 625 |