Digitális szűrők

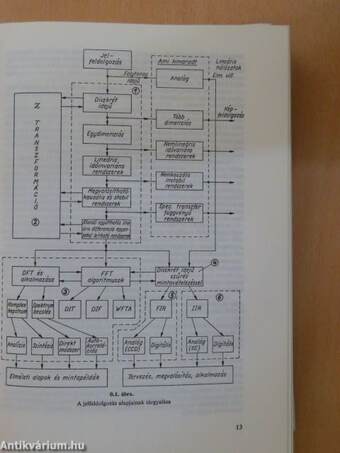
A digitális jelfeldolgozás alapjai

Szerző

Dr. Simonyi Ernő

Szerkesztő

Mózer István

Lektor

Dr. Sallai Gyula

Budapest

'Dr. Simonyi Ernő: Digitális szűrők ' összes példány

Kiadó:	Műszaki Könyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1984
Kötés típusa:	Vászon
Oldalszám:	563 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	25 cm x 12 cm
ISBN:	963-10-5306-7
Megjegyzés:	276 fekete-fehér ábrával illusztrált. Tankönyvi szám: 61134.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Előszó	11
Diszkrét idejű jelek és rendszerek	17
Bevezetés	17
Alapelemek: sorozatok és műveletek	19
Elemi jelsorozatok	19
Alapműveletek	20
Elsőfokú diszkrét idejű rendszer	22
Az elsőfokú diszkrét idejű rendszer analóg és digitális megvalósítása	23
A diszkrét idejű rendszerek leírása	26
A lineáris és időinvariáns rendszerek jellemzése	27
A konvolúciós összeg tulajdonságai és kiszámítása	28
Az egységimpulzus-válaszfüggvény és a transzferfüggvény	33
Kauzalitás és stabilitás	36
Lineáris állandó együtthatós differenciaegyenletek	38
A kauzális hálózatok egyértelmű leírása	38
A differenciaegyenletek megoldása	39
Az elsőfokú differenciaegyenlet megoldása	40
A másodfokú differenciaegyenlet megoldása	41
A diszkrét idejű szűrők osztályozása	43
A FIR és az IIR szűrők osztálya	43
Rekuzív és nemrekurzív rendszerek	44
ARMA típusú rendszerek	45
Az osztályozások kapcsolatrendszere	45
Frekvenciatartományi leírás	47
A z-fázissík használata	48
Frekvenciaválasz-függvény	49
Példák	50
Diszkrét sorozatok Fourier-transzformációja	53
Fourier-transzformált párok	53
Konvergeciafeltételek	54
Frekvenciatartományú átvitel	56
Szimmetriatulajdonságok	57
Periodikus sorozatok diszkrét Fourier-sora	59
A Fourier-soroktól a diszkrét Fourier-sorokig	60
A diszkrét Fourier-sor (DFS) pár	61
A diszkrét Fourier-sorok tulajdonságai	62
Periodikus konvolúció	63
A diszkrét -Fourier-transzformáció alapjai	65
A DFS és a DFT kapcsolata	65
A DFT mint alapművelet	66
Az EFT eljárás	68
Gyors konvolúció a DFT használatával	70
Összefoglalás	72
A Z-transzformáció és alkalmazása	75
Bevezetés	75
A z-transzformáció alapjai	76
Definíció	76
A z-transzformáció mint Laurent-sor	77
A z-transzformáció mint a Fourier-transzformáció általánosítása	80
z-ben racionális törtfüggvények	81
A z-transzformált meghatározása	83
A z-transzformáció alaptételei	83
Differenciálási, integrálási és konvolúciós tételek	85
Kezdeti és végérték, valamint összegezési tételek	87
A z-transzformált számítása a Laplace-transzformáltból	90
Az inverz z-transzformáció	94
Alapösszefüggések	94
A reziduumtétel alkalmazása	95
Részlettörtekre bontás	97
Hatványsoros közelítés	98
A komplex konvolúció és alkalmazása	100
Sorozatok szorzatának z-transzformációja	100
Parseval-reláció	103
Ablakozás a komplex konvolúcióval	104
Kauzális sorozatok z-transzformáltja	105
A diszkrét idejű transzferfüggvény	107
Stabil rendszerek	107
Kauzális sorozatok és transzferfüggvények	108
Differenciaegyenletek z-transzformációja	109
A pólusok és az idősorozatok kapcsolata	110
A z-transzformált mintavételezése	111
A z-transzformált és a DFS együtthatók kapcsolata	112
A z-transzformált inverz DFS sorozata	114
A z-transzformált előállítása egységkörű mintáiból	115
A Fourier-transzformált mintavételezése	116
A transzverfüggvényeket közvetlenül megvalósító alapkapcsolások	118
Direkt formájú IIR kapcsolások	118
Első- és másodfokú alaptagokból felépített IIR szűrú	120
Transzverzális FIR szűrú struktúrák	123
Interpoláló FIR szűrő struktúrák	125
Analízis a z-transzformációval	127
z tartományú állapotváltozós analízis	127
Racionális törtfüggvények stabilitásanalízise	129
Frekvenciatartományú analízis	131
Időtartományú analízis	133
Összefoglalás	134
A diszkrét Fourier-transzformáció és alkalmazása	137
Bevezetés	137
DFT a véges hosszúságú sorozatok leírására	138
A DFT és az inverz DFT definíciója	140
A DFT és a z-transzformált kapcsolata	142
A DFT és szimmetriatulajdonságai	143
A cirkuláris eltolási tétel	147
Konvolúció és korreláció a DFT segítségével	151
A cirkuláris konvolúció	151
Lineáris konvolúció a cirkuláris konvolúcióból	153
Szakaszolt konvolúció	156
Korrelációs tétel	159
A diszkrét Hilbert-transzformáció	162
A Fourier-transzformált valós és képzetes részének kapcsolata	162
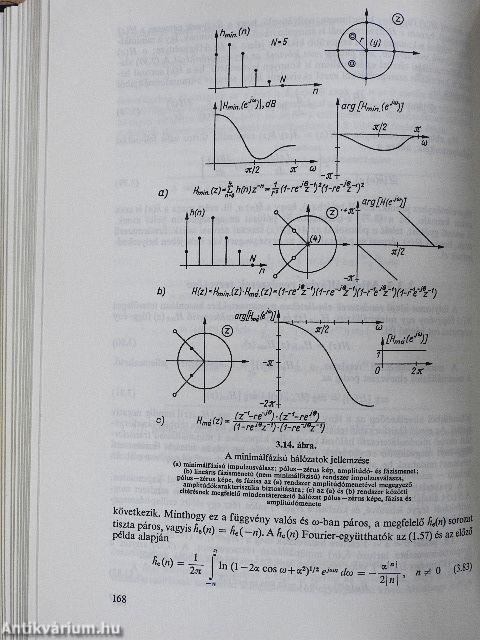
A minimálfázisú feltétel	165
Minimálfázisú rendszerek tervezése	167
Komplex sorozatok Hilbert-transzformációja	170
A homomorfikus jelfeldolgozás és alapelemei	172
Összeszorzott sorozatok szétválasztása	173
Dekonvolúció a komplex kepstrum használatával	174
Komplex és valós kepstrum kapcsolata	177
A homomorfikus dekonvolúció alkalmazásai	179
A DFT meghatározása FFT algoritmussal	182
A DFT redundanciája	183
Az FFT algoritmusok alapgondolata	185
Az R2 DITI FFT algoritmus	187
A helyben számolás megkötése	189
Az FFT algoritmusok általános algebrai formája	190
Az FFT algoritmusok osztályozási szempontjai	190
Az általánosítás megalapozása bináris indexeléssel	191
A Cooley-Tukey-féle DIT2 FFT algoritmus	195
A DIT FFT algoritmusok általános algebrai egyenletei	197
Az FFT algoritmusok családjai	198
A helyben számoló DIT algoritmusok	199
Nem helyben számoló DIT algoritmusok	200
A DIF algoritmusok származtatása	201
WFTA: A Winograd-féle FFT algoritmus	204
A teljesítményspektrum becslése	210
Determinisztikus és sztochasztikus jelek spektruma	210
A direkt módszerek	215
Az autokorrelációs módszer	217
Valós sorozatokon végzett FFT műveletek	220
Összefoglalás	222
Analóg jelek digitális feldolgozása	225
Bevezetés	225
A folytonos idejű jelek spektrális tulajdonságai	230
A Fourier-integrálok tételei	233
A Dirac-delta függvény	238
Periodikus jelek Fourier-sorainak származtatása	242
A Gibbs-oszcilláció	244
A mintavételezés alapjai	248
Az ideális mintavételezés	250
A mintavételezési tétel	253
Sávszűrt jelek mintavételezése	255
Nemideális mintavételezés	258
A Laplace- és z-transzformáltak kapcsolata	261
A mintavételezett jelek Laplace-transzformáltja	264
A z-transzformált meghatározása	266
A mintavételezett jel pólus-zérus képe	268
A komplex s és z síkok kapcsolata	270
A folytonos és diszkrét idejű Fourier-analízisek kapcsolata	272
A poisson-összegzés formula	272
A Fourier-integrál kiértékelésének főtétele	274
A folytonos és diszkrét idejű Fourier-transzformáltak kapcsolata	276
A Fourier-sorok és a DFT kapcsolata	278
Analóg jelek diszkrét idejű feldolgozása	280
Diszkrét idejű emuláció és szimuláció	281
Szimulációs tétel	283
Funkcionális blokkdiagram	285
A négyszögimpulzus-sorozat diszkrét idejű szűrése	286
A/D és D/A átalakítás	289
Kódkonverziók	291
A mintavételezés dzsitterzaja	295
Az A/D átalakítás kvantálási zaja	297
A D/A átalakító jelének visszaállítása szűréssel	300
Számábrázolás és kvantálás a digitális szűrőkben	302
Fixpontos számábrázolás	302
Lebegőpontos számábrázolás	303
Kvantálási típusok	304
A csonkítás és a kerekítés hatása	305
Decimálás és interpolálás	308
Decimálás egész számmal	309
A decimálás alkalmazási példája FDM demoduláció	311
Interpolálás egész számmal	313
Decimálás és interpolálás törtszámmal	315
Összefoglalás	318
Véges impulzusválaszú (FIR) szűrők tervezése és alkalmazása	321
Bevezetés	321
A lineáris fázisú FIR szűrők általános jellemzése	324
A lineáris fázismenet feltételei	324
Szimmetikus és antiszimmetikus impulzusválaszok	326
Lineáris fázisú FIR szűrők frekvenciaválasza	327
Pólus-zérus kép	330
Tervezés ablakozási módszerekkel	332
Az ablakozás alapelvei	333
Ablakozófüggvények	335
A Kaiser-féle ablak és használata	340
Gyakorlati tervezési példák	344
Interpolációs tervezés	349
Alapelvek	350
Optimalizálási lehetőségek lineáris programozással	353
A tervezés menete	357
Tervezési példa	359
Optimális FIR szűrők tervezése	361
Súlyozott csebisev-féle approximáció	362
A Remez-féle kicserélési algoritmus	366
Tervezés a Remez-algoritmussal	367
Tervezési példák	369
Diszkrét analóg megvalósítás és problémái	375
A töltéscsatolt eszközök (CCD) működési elve	378
A CCD elemek alkalmazási korlátai	381
CCD transzverzális szűrők tervezése	385
A transzverzális szűrő együttható-toleranciáinak hatása	389
Diszkrét analóg CCD szűrők alkalmazásai	393
Az illesztett szűrők	395
A Cirp z-transzformációs (CZT) alkalmazások	396
Programozható és változtatható transzverzális szűrők	400
Precíziós alkalmazások	403
Digitális megvalósítás és problémái	405
Számítástechnikai és hardverkomplexitás	405
digitális FIR szűrők koncentrált aritmetikával	408
Digitális szűrők elosztott aritmetikával	410
Az együtthatók véges szóhosszúságának hatása	415
Digitális alkalmazások	417
Időosztásos FIR szűrőblokk	417
Decimálás és interpolálás	420
SSB moduláció Hilbert-transzformátorral	422
Szűrőélesítés	424
Összefoglalás	426
Végtelen impulzusválaszú (HR) szűrők tervezése és alkalmazása	129
Bevezetés	429
IIR szűrők tervezése analóg szűrők transzformációjával	431
Az impulzus invariáns transzformáció	433
Az illesztett z-transzformáció	436
Az Euler-és Bruton-leképzések	438
Digitális frekvenciatranszformációk	443
Tervezés a bilineáris transzformációval	445
Alaptulajdonságok	447
A H(z) függvény előállítása és megvalósítása	450
Transzformációs összefüggések	455
Általános karakterisztika tervezése optimalizálással	460
Diszkrét idejű hullámszűrők	462
Hullámszűrő hatásgráfjának alapelemei	465
Összekapcsolási szabályok	469
Az igazi létrahullámszűrő	471
Tervezési példák	474
A diszkrét idejű leapfrog-szűrők	479
Aktív RC leapfrog-aluláteresztő	484
Elliptikus aluláteresztő és sávszűrő leapfrog	487
Áttérés a diszkrét idejű tartományra	488
Az LDI leapfrog lezárási problémái	492
Diszkrét analóg megvalósítás és problémái	492
Technológiai korlátok	494
SC alapelemek	498
SC integrátorok	502
Bilineáris SC elemek	506
Diszkrét analóg SC szűrők alkalmazásai	508
Csbisev aluláteresztő SC leapfrog-szűrők	511
Elliptikus aluláteresztő és sávszűrő SC leapfrog	512
Bikvadratikus kaszkád alaptagokból felépített SC szűrők	518
Időmultiplexelt SC szűrők	521
Digitális megvalósítás és problémái	524
Az együtthatók véges szóhosszúságának hatása	526
A műveletvégzők kvantálási zaja	529
Skálázási eljárások	531
Nulla bemenetű határoszcilláció	535
Digitális alkalmazások	535
Digitális IIR struktúrák összehasonlítása	540
Digitális LDI leapfrog-szűrő	543
Transzmultiplexek működési elvei	545
Digitális Weaver SSB modulátor	548
Függelék	551
Irodalomjegyzék	553
Tárgymutató	560

Témakörök

Műszaki > Informatika > Egyéb
Műszaki > Elektronika > Egyéb

Dr. Simonyi Ernő

Dr. Simonyi Ernő műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Simonyi Ernő könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem