Ismerkedés a topológiával

Szerző

Papy

Fordító

Márki László

Lektor

Dr. Bognár Mátyás

Budapest

'Papy: Ismerkedés a topológiával ' összes példány

Kiadó:	Műszaki Könyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1973
Kötés típusa:	Fűzött kemény papírkötés
Oldalszám:	259 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	21 cm x 15 cm
ISBN:
Megjegyzés:	Színes és fekete-fehér illusztrációkat tartalmaz. Tankönyvi szám: 60507.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Előszó	8
Előszó a magyar kiadáshoz	10
Bevezetés
Halmazok	13
Még mindig halmazok	19
Relációs kisszótár	21
Röviden a relációkról	36
Halmazelméleti szemlélet a sík geometriájában	38
A számegyenes. R ->R függvények	42
Távolság a síkban	48
A számosság fogalma	52
Néhány egyszerűbb számosság	55
Kvantorok	61
Általános topológia a síkban
Bevezetés	67
Pí nyílt halmazai	68
Zárt halmazok	74
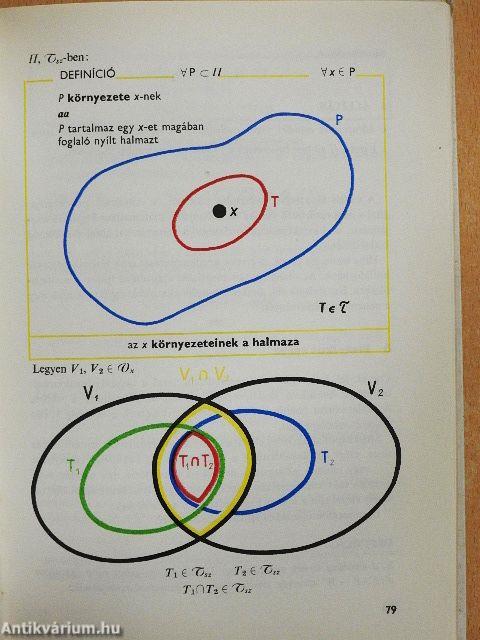
Környezetek	78
Metrikus terek	80
Topologikus terek	82
Szétválasztás	84
Zárt halmazok és környezetek	86
A topologikus tér alterei	87
A topológia bázisai	93
Halmazok lezárása	96
Környezetbázis	101
Az elemi analízis topologikus terei
Az izomorfizmus általános fogalma	107
Homeomorfizmusok	107
Homeomorfizmusok és bázisok	108
Topologikus terek automorfizmusai	109
Alterek homeomorfizmusai	110
Topológia átvitele bijekcióval	110
R intervallumai	112
R minden nem üres, nyílt intervalluma homeomorf R-rel	113
R (nem egyelemű) zárt szakaszainak (szokásos) topológiája	113
Az R bővített számegyenes	114
Elbűvölő módszer a 15. pont eredményeihez	121
Két topologikus tér szorzata	123
Homeomorfizmus és topologikus terek szorzata	128
Az R + és * műveletei értelmezési tartományául szolgáló topologikus tér	129
A kettős sorozatok vizsgálatára szolgáló topologikus tér	132
Folytonosság
A folytonosság hozzávetőleges fogalma a köztudatban	135
A folytonos szó	138
Jordan-ívek és kontinuum számosság	139
Jordan-ívek és folytonos függvények	140
A sík transzformációinak folytonossága	141
Globális folytonosság	141
Lokális folytonosság	146
Egy pontban folytonos függvény	147
A pí sík transzformációi	153
Topologikus terek leképezései	159
Környezetbázisok	161
Környezetek ősképe	163
R-ből R-be vezető függvények	164
Kompozíció	168
Nyílt halmazok ősképe	169
A folytonosság belső jellege	172
Az egy pontban való folytonosság lokális jellege	173
Topologikus terek szorzata	175
Az analízis egy alapvető tételéről	176
Gyakorlatok	180
Folytonos függvények és folytonos ívek
R-ból R-ba vezető folytonos függvények	187
Leképezés bijekciója	188
Folytonos ívek vagy Jordan-ívek	192
Cantor-féle triadikus halmaz	196
Cantor-féle szuperjekciók	198
Bal oldali és jobb oldali folytonosság	202
PEANO tétele (1890)	203
Kompaktság
Kompakt halmazok R-ben	214
Kompakt terek	215
BOREL-LEBESGUE tétele	219
Kvázi-kompakt halmazok és zárt halmazok	224
Kvázi-kompakt terek folytonos képe	227
Folytonosság és kompaktság	229
A kompakt topológiák kettős extremális tulajdonsága	230
A gyakorlatok megoldása	237
Jelmutató	253
Tárgymutató	257