1.127.280
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Komplex rendszerek vizsgálata
Összemérési módszerek
| Kiadó: | Műszaki Könyvkiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött keménykötés |
| Oldalszám: | 262 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | 963-10-1830-x |
| Megjegyzés: | Fekete-fehér ábrákkal illusztrált. Tankönyvi szám: 41700 |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Előszó | 9 |
| Bevezetés | 11 |
| A komplex rendszerek összemérési problémái | 16 |
| Mérés- és skálaelméleti alapismeretek | 17 |
| Névleges (nominális) skála | 20 |
| Sorrendi (ordinális) skála | 21 |
| Intervallumskála | 22 |
| Aranyskála (abszolút skála) | 23 |
| Értékelő megjegyzések | 24 |
| A tulajdonságok megválasztása | 27 |
| Az értékelési tényezők súlyozása | 31 |
| Súlyozás sorrendi skálán | 32 |
| Súlyozás intervallumskálán | 35 |
| A súlyozási eljárás megválasztásának szempontjai | 51 |
| A komplex rendszerek értékelési tényezők szerinti preferenciasorrendje | 52 |
| Az egyes értékelési tényezők szerinti preferenciasorrend | 54 |
| Több értékelési tényező szerinti preferenciasorrend | 57 |
| Az előnyök és hátrányok mérlegelése | 65 |
| Komplex rendszerek egyes összemérési módszerei | 68 |
| A módszer fogalma és lényeges vonásai | 68 |
| Harris és Marting módszere | 71 |
| JUHAR módszer | 73 |
| Pareto elemzés (ABC elemzés9 | 74 |
| Kesselring módszere | 76 |
| Az összehasonlító jellemző módszere | 79 |
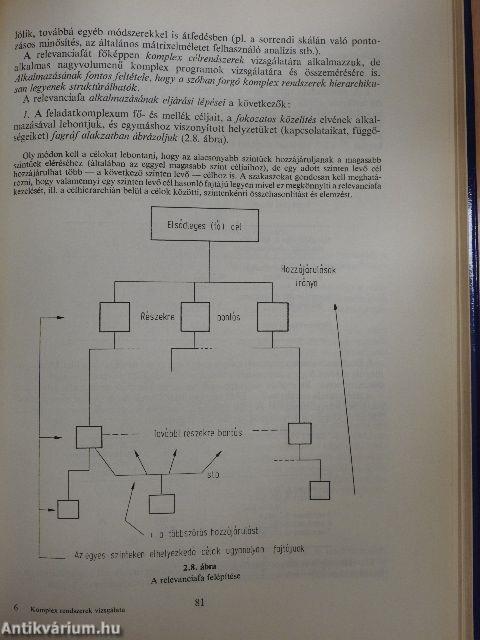
| A relevanciafa módszere (PATTERN) | 80 |
| Cross-impact elemzés | 83 |
| Bridgman módszere | 86 |
| A Kendall-féle rangkorrelációs módszer | 91 |
| Normál eset (nincs kötés) | 92 |
| Rangszámegyezés esete (kötések) | 94 |
| Combinex módszer | 95 |
| MARSAN módszer és az ELECTRA program | 97 |
| KIPA módszer | 103 |
| Ordinális programozás | 115 |
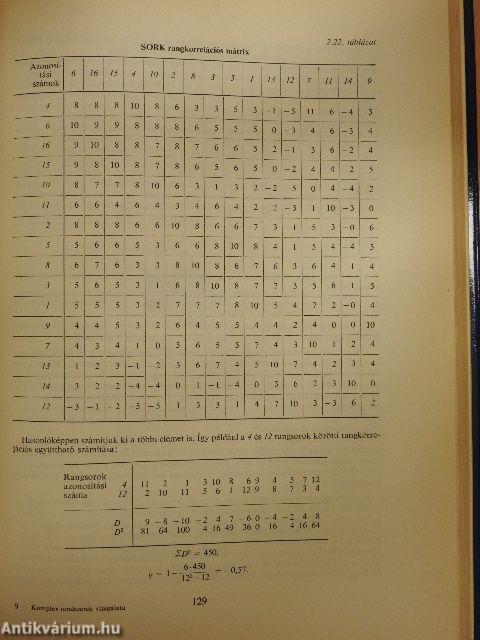
| SORK módszer | 125 |
| Clusteranalízis | 135 |
| V-analízis | 137 |
| O-analízis (tipológia) | 139 |
| Kassay módszere | 142 |
| Lagrange-féle szorzók módszere | 144 |
| A módszer megválasztása | 148 |
| A KIPA módszer részletesebben | 151 |
| Eljárástechnikai megoldások | 175 |
| A párok optimális elrendezése a páros összehasonlítás során | 175 |
| A Kendall-féle rangkonkordancia együttható szignifikanciavizsgálata | 179 |
| A következetesség szignifikanciavizsgálata | 181 |
| A Kendall-féle egyetértési együttható szignifikanciavizsgálata | 187 |
| Függelék | 192 |
| Beruházási változatok vizsgálata KIPA módszerrel | 192 |
| A beruházások jellemzőinek meghatározása és az összehasonlított változatok tényezőnkénti rangsora | 194 |
| Az értékelés szintézise, az összehasonlított változatok eredő rangsorának meghatározása | 198 |
| A vállalati beruházások megalapozásának és előkészítésének folyamata | 201 |
| A döntéselőkészítés feladatainak megosztása | 201 |
| A beruházási javaslatok tárcaszintű elbírálásának rendszere | 202 |
| Értékelési tényezők a beruházási programok elbírálásához, összehasonlításához és rangsorolásához | 205 |
| A KIPA módszer alkalmazása a vállalati célok meghatározásánál | 207 |
| A felsőbbszintű és hosszabbtávú stratégiai döntések megalapozásának problémái és lehetőségei | 209 |
| Példa a vállalatpolitikai változatok értékelésére | 209 |
| Gazdasági szervezetek minősítése KIPA módszerrel | 211 |
| Gyártmánystruktúra és gyártmányszínvonal vizsgálatok | 219 |
| Gyártmánystruktúra és gyártmányszínvonal vizsgálat KIPA módszerrel | 219 |
| Következtetések a termelés, ill. a kereskedelem fejlesztésére - a vizsgált termékek komplex értékelése alapján | 224 |
| Gyártmányszínvonal vizsgálata sütőipari termékek minősítésére | 227 |
| Egyéb alkalmazási példák (termelésprogramozás, munkakörértékelés, szakemberek minősítése) | 230 |
| Programrendszerek termelőberendezések extenzív és intenzív kihasználására | 230 |
| Feldolgozástechnikai eljárások összehasonlítása | 233 |
| Munkakörök értékelése | 234 |
| Példa a KIPA módszer egyik moduljának önálló alkalmazására | 238 |
| A bírálók minősítésének egyszerűsített módszere | 241 |
| Bírálók minősítése a Kendall módszer felhasználásával | 243 |
| Az együtthatók kiszámítása és az eredmények értékelése | 243 |
| Néhány egyszerű bizonyítás | 246 |
| Az inkonzisztens körhármasok kérdéséhez | 246 |
| A körhármasok maximális számának bizonyítása | 247 |
| A körhármasok maximális megállapítása | 247 |
| A körhármasok számának megállapítása | 249 |
| A Kendall-féle rangkonkordancia együttható Delta-m mennyiségének meghatározása | 249 |
| A teljes ellentét bizonyítása | 250 |
| Irodalomjegyzék | 252 |
| Tárgymutató | 259 |
Témakörök
Megvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.