Lineáris programozás

Szerző

Szerkesztő

Lektor

Budapest

'Krekó Béla: Lineáris programozás ' összes példány

Kiadó:	Közgazdasági és Jogi Könyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1962
Kötés típusa:	Vászon
Oldalszám:	411 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	20 cm x 15 cm
ISBN:
Megjegyzés:	Fekete-fehér ábrákkal illusztrálva.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

A lineáris programozás technikája
Bevezetés	21
A programozásról általában	21
Példák a lineáris programozásra	29
Mi tehát a lineáris programozás?	29
Történeti megjegyzések	32
A szállítási probléma	33
A probléma megfogalmazása	33
A költségmatrix átalakítása	35
Az induló program	38
A program javítása	41
A potenciálok módszere	45
Alternatív lehetőségek az optimalizálásban	50
Névleges állomások beiktatása	51
Korlátozó feltételek	55
Közelítő megoldás	56
A szimplex-módszer	64
A normál-feladat	64
Az induló program	65
A program javítása	67
Van-e mindig megoldás?	80
A degeneráció	81
Alternatív optimumok	86
A módosított normál-feladat	90
Az általános eset	95
A dualitás	103
Speciális problémák	111
Egy szállítási feladat módosítása	111
Számolás korlátozott változókkal	115
Számolás nem korlátozott változókkal	119
Egy ellenőrzési lehetőség	121
Variánsszámítás szimplex-módszerrel	124
A parametrikus programozás	129
A konvex programozásról	137
A lineáris programozás matematikai alapjai
Halmazelméleti alapfogalmak	147
Halmazok	147
Részhalmazok	148
Műveletek halmazokkal	148
Az alaphalmaz	150
A lineáris tér	151
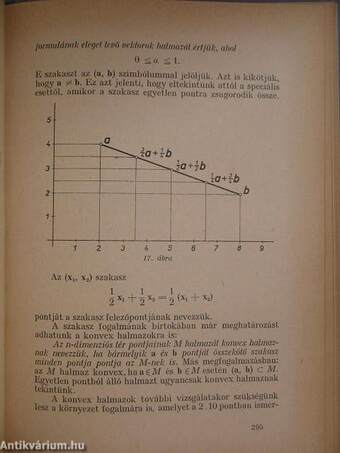
Vektorok	151
Nagyságrendi relációk és műveletek	155
A lineáris tér definíciója	157
Lineáris kombinációk	158
Az altér fogalma	159
Lineárisan független vektorok	160
A vektorrendszerek rangja	164
A dimenzió és a bázis	168
Az n-elemű vektorok tere	169
Az euklideszi tér	171
Matrixok	175
A matrix fogalma	175
Nagyságrendi relációk és műveleti szabályok	179
A matrixok rangja	187
A matrixok felbontása blokkokra	189
A lineáris térrel kapcsolatos numerikus számításokról	192
Az elemi transzformáció	192
A kompatibilitás	199
A matrixok rangjának meghatározása	201
Egy speciális faktorizáció	203
Lineáris egyenletrendszerek megoldása és matrixok inverziója	207
Általános tudnivalók	207
A lineáris egyenletrendszerek megoldása	208
A matrixok inverze	214
Az inverz numerikus meghatározása	217
A vektorcseréről általában	222
A lineáris programozás	227
A probléma megfogalmazása	227
A megoldás feltételéről	228
A normál-feladat	234
A degeneráció	239
A módosított normál-feladat	242
Az általános eset	245
Az optimális programok halmaza	247
A szállítási probléma	250
A feladat megfogalmazása	250
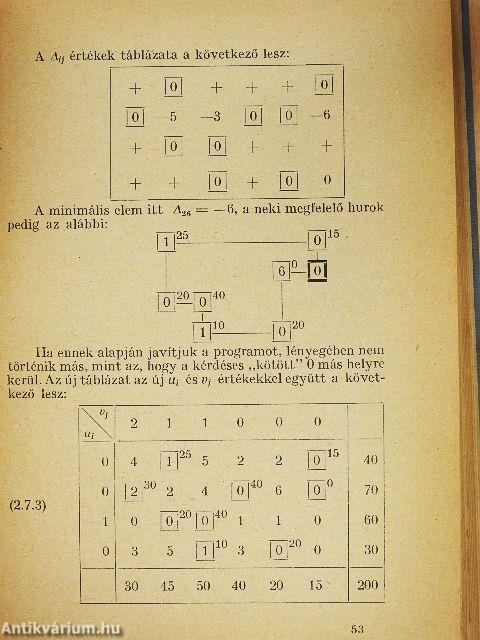
Lépcső, bázis és hurok	253
Az induló program	258
A program javítása	260
A módosított szimplex-módszer és a parametrikus programozás	263
A módosított szimplex-módszer	263
Variánsszámítás	268
A parametrikus programoz ás	271
A lineáris programozás és a játékelmélet	276
A játékelmélet alapfogalmai	276
Néhány alapvető tétel	278
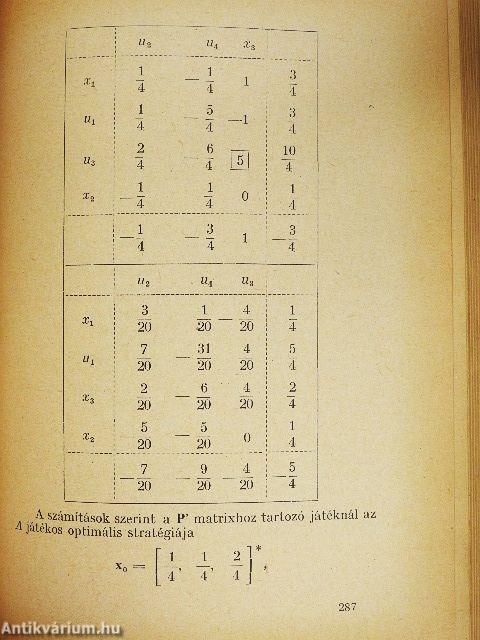
Neumann tétele	282
Numerikus példa	285
A lineáris programozás mint a játékelmélet speciális esete	288
Néhány megjegyzés a játékelmélethez	293
A lineáris programozás geometriai háttere	294
A konvex halmazokról	294
A lehetséges megoldások halmaza	297
Az optimális megoldások halmaza	307
A szimplex-módszer interpretációja	310
Néhány szó a megoldás egyéb módszereiről	311
Gyakorlati alkalmazások
Az alkalmazás feltételei	315
Numerikus példák	319
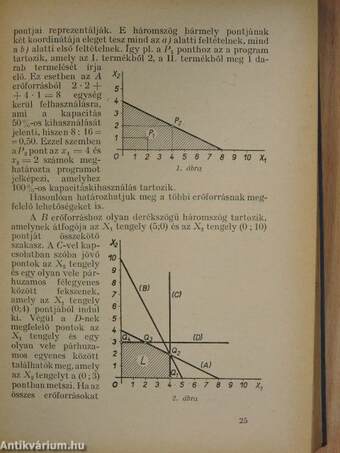
Egy összetett szállítási probléma	319
Termelési programok összekapcsolása szállítási programokkal	323
Egy termelési probléma	327
Egy speciális gépterhelési feladat	332
Hengersorok programozása	337
Egy Kantorovics-féle probléma	341
Alternatív technológiák	342
Egy mezőgazdasági alkalmazás	344
Optimális létszám-probléma	347
Egy áruellátási probléma	349
Minimális vágási veszteség	354
Néhány probléma általános tárgyalása	357
A gépterhelési probléma általánosítása	357
Kantorovics feladata	359
A magyar papíripar modellje	360
Ágazati kapcsolatok elemzése	365
Függelék
A magyar módszer	373
A hozzárendelési probléma	373
A szállítási probléma	386
A Kőnig - Egerváry-féle tétel	391
A független pontok és a fedővonalak megkeresése	393
Az iteráció matematikai indokolása	395
Irodalomjegyzék	401
Tárgymutató	408