1.120.057
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Matematika híradástechnikusoknak
| Kiadó: | Műszaki Könyvkiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Félvászon |
| Oldalszám: | 383 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 18 cm |
| ISBN: | |
| Megjegyzés: | Tankönyvi szám: 674. Fekete-fehér ábrákkal. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Tartalom
| Az első kiadáshoz írt előszóból | 3 |
| Előszó a második kiadáshoz | 4 |
| Bevezetés | 11 |
| Aritmetika és algebra | |
| Számok és mennyiségek | |
| A szám fogalma | 13 |
| A mennyiség fogalma | 13 |
| Alapmennyiségek és dimenziórendszerek | 14 |
| Skaláris- és vektormennyiségek | 15 |
| Szám- és mennyiségegyenes | 15 |
| Tizes számrendszer | 16 |
| A számok helyettesítése betűkkel, képletjelek | 16 |
| Fizikai mértékegységek és mértékrendszerek | 18 |
| Alapműveletek | |
| Összeadás | 20 |
| Kivonás: negatív számok | 22 |
| Szorzás: zárójelek | 23 |
| Osztás: törtek | 27 |
| Hatványozás és gyökvonás | |
| Pozitív, egészkitevőjű hatványok | 31 |
| Zérus és negatív egészkitevőjű hatványok | 33 |
| A hatványozás alkalmazásai | 34 |
| Binom | 37 |
| A gyökvonás és a törtkitevőjű hatvány fogalma | 38 |
| Műveletek gyökmennyiségekkel | 40 |
| A gyök többértékűsége | 42 |
| Negatív számok négyzetgyöke. Képzetes számok | 42 |
| Elsőfokú algebrai egyenletek. Determinánsok | |
| Az egyenlet fogalma és osztályozása | 43 |
| Fizikai egyenletek | 44 |
| Elsőfokú egyismeretlenes egyenletek | 45 |
| Elsőfokú kétismeretlenes egyenletrendszer | 48 |
| Elsőfokú többismeretlenes egyenletrendszer | 51 |
| Determinánsok | 53 |
| Magasabb fokú algebrai egyenletek | |
| Egyismeretlenes másodfokú egyenletek | 60 |
| Többismeretlenes másodfokú egyenletek | 63 |
| Magasabb fokú egyenletek | 64 |
| Algebrai függvények | |
| A függvény fogalma. Egyváltozós függvények ábrázolása | 68 |
| A függvényfogalom fizikai és műszaki alkalmazása | 71 |
| Kétváltozós függvények | 73 |
| Egyváltozós algebrai függvények osztályozása | 75 |
| Racionális egészfüggvények | 76 |
| Racionális törtfüggvények | 81 |
| Irracionális függvények | 82 |
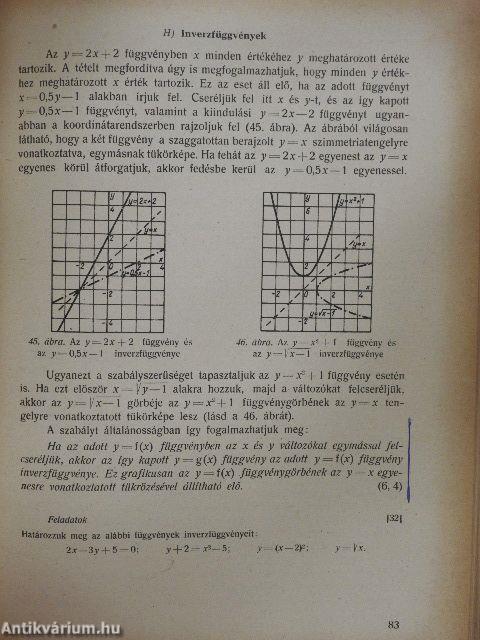
| Inverzfüggvények | 83 |
| A geometria alapjai | |
| Geometriai alapfogalmak | |
| Bevezetés | 84 |
| A geometria alapelemei | 85 |
| Szerkesztési segédeszközök | 86 |
| Terület- és térfogatszámítás | 88 |
| A síkgeometria axiomái | 89 |
| Egyenes szakaszokkal határolt síkidomok | |
| Pont és egyenes | 89 |
| Háromszögek | 92 |
| Derékszögű háromszögek | 94 |
| A háromszög területe | 96 |
| A háromszög nevezetesebb tételei | 97 |
| Négyszögek | 98 |
| Sokszögek | 101 |
| Trigonometria. Egyenesekkel határolt síkidomok analitikus tárgyalása | |
| Szögfüggvények | 102 |
| Szögfüggvények közötti összefüggések | 105 |
| Szögfüggvények grafikus ábrázolása | 107 |
| Két egyenessel bezárt szög. Az egyenes iránytényezője | 108 |
| Egyenesekkel határolt síkidomok analitikus tárgyalása | 110 |
| Kúpszeletek | |
| Általános alapfogalmak | 111 |
| A kör | 112 |
| Polárkoordináták | 117 |
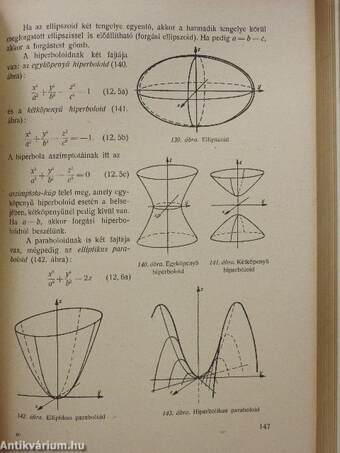
| Az ellipszis | 118 |
| A hiperbola | 121 |
| A parabola | 125 |
| A szögfüggvények általánosítása | |
| A szögfüggvények értelmezésének kiterjesztése. A szögfüggvények fogalma | 126 |
| Periodikus fizikai jelenségek | 131 |
| Trigonometrikus függvények összeadási, szorzási és hatványozási szabályai | 134 |
| A trigonometriai összefüggések alkalmazásai | 137 |
| A térgeometria alapjai | |
| Kétváltozós függvények térbeli ábrázolása | 145 |
| Szögletes testek | 148 |
| Henger, kúp, gömb | 151 |
| Gömb- és hengerkoordináták | 153 |
| Geometriai vonatkozású rádiótechnikai feladatok | |
| Két párhuzamos ellenállás eredőjének grafikus meghatározása | 154 |
| Fázisban eltolt váltakozó feszültségek ábrázolása | 155 |
| Hegyesszögű háromszög meghatározása | 158 |
| Komplex-számok ábrázolása | 160 |
| Árkuszfüggvények | 162 |
| Ábrázoló geometria és műszaki rajzok | |
| Az ábrázoló geometria alapjai | 163 |
| Műszaki rajzok | 165 |
| Analízis | |
| Az analízis alapjai | |
| Bevezetés | 169 |
| Matematikai függvények osztályozása | 169 |
| Sorok | 170 |
| Sorok konvergenciája | 172 |
| Fontosabb határértékek. Az e természetes szám | 174 |
| Függvények folytonossága | 176 |
| Exponenciális, hiperbolikus és logaritmus függvények | |
| Exponenciális függvények | 177 |
| Logaritmus függvények I. | 177 |
| Logaritmus függvények II. | 181 |
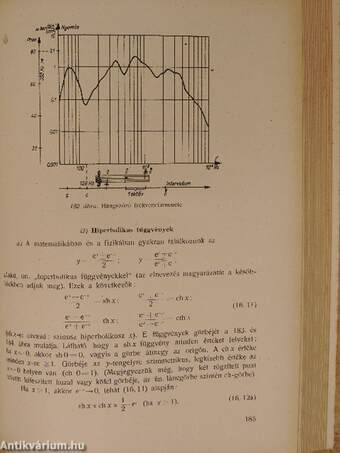
| Hiperbolikus függvények | 185 |
| Áreafüggvények | 188 |
| Az első differenciálhányados | |
| Alapfogalmak | 188 |
| Derivált függvény grafikus ábrázolása | 190 |
| Egyszerű differenciálási szabályok | 191 |
| Hatványok deriválása | 192 |
| Függvények szorzatának és hányadosának deriválása | 194 |
| Transzcendens függvények deriválása | 195 |
| Inverz függvények deriválása | 197 |
| Összetett függvény (láncfüggvény) deriválása | 198 |
| Hiperbolikus- és áreafüggvények deriválása | 200 |
| Magasabb és parciális deriváltak | |
| A második differenciálhányados | 201 |
| Magasabb deriváltak | 202 |
| Maximum, minimum, inflexiós pont | 203 |
| Parciális deriválás: implicit függvények | 206 |
| Taylor- és Mac Laurin-sorok | |
| Differenciálható függvények előállítása egészfüggvényekkel | 210 |
| Mac Laurin-sor | 212 |
| A Mac Laurin-sor alkalmazásai | 214 |
| Taylor-sor | 217 |
| A Taylor-sor alkalmazásai | 218 |
| A differenciálfogalom fizikai alkalmazásai | |
| A differenciálegyenlet fogalma | 222 |
| Mozgásjelenségek | 222 |
| Elektrotechnikai feladatok | 225 |
| Parciális differenciálegyenletek | 227 |
| Az integrálszámítás alapjai | |
| Az integrál fogalma | 227 |
| Egyszerű integrálási szabályok | 230 |
| Különleges integrálási módszerek | 233 |
| Algebrai függvények integrálása | 236 |
| Transzcendens függvények integrálása | 239 |
| A határozott integrál | |
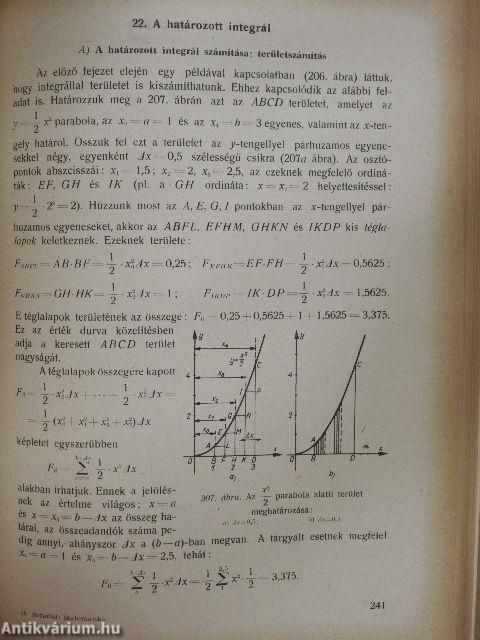
| A határozott integrál számítása; területszámítás | 241 |
| Hiperbolikus függvények | 244 |
| A határozott integrál további alkalmazásai | 246 |
| Differenciálegyenletek megoldásai | |
| Egyszerűbb differenciálegyenletek | 249 |
| Homogén lineáris differenciálegyenletek | 251 |
| Inhomogén lineáris differenciálegyenletek | 255 |
| Magasabbrendű lineáris differenciálegyenletek teljes megoldása. Euler-egyenlet | 256 |
| Fourier-sorok | |
| A sor előállítása | 260 |
| A Fourier-sor alkalmazásai | 260 |
| Szimbolikus számítási módszer | |
| A szimbolikus számítási módszer alapfogalmai | |
| Bevezetés | 264 |
| Szinuszrezgés szimbolikus ábrázolása | 264 |
| Az Euler-egyenletből folyó következtetések | 265 |
| Forgó és nyugvó vektorok | 268 |
| A szimbolikus módszer alkalmazhatósága | 270 |
| Számolási műveletek nyugvó vektorokkal | 273 |
| Változó vektorok | 279 |
| Komplex-vektorok helyzetgörbéi | 280 |
| Egyszerűbb váltalkozóáramú feladatok szimbolikus tárgyalása | |
| Alapfogalmak; passzív kétpólusok | |
| Váltakozóáramú mennyiségek szimbolikus alakja | 287 |
| Komplex-ellenállások | 287 |
| Komplex-vezetések | 291 |
| Passzív kétpólusok | 292 |
| Egyszerűbb váltakozóáramú feladatok szimbolikus tárgyalása (Rezgőkörök; aktív kétpólusok) | |
| Rezgőkörök | 300 |
| Aktív kétpólusok | 303 |
| Hálózatok | 311 |
| Négypólusok | |
| Alapfogalmak | 314 |
| Üresjárási, rövidzárási ellenállás és vezetés | 315 |
| Bemenő-, kimenőimpedancia és admittancia | 316 |
| Karakterisztikus impedancia és admittancia | 318 |
| Áram- és feszültségviszonyok | 321 |
| Áttételi viszonyok, átviteli mérték | 323 |
| Nem-stacionárius jelenségek | |
| Vezetéken kialakuló hullámok | 329 |
| Nem-stacionárius kapcsolási elemek (vezetékek) | 335 |
| A szimbolikus módszer további alkalmazásai | |
| Lineáris differenciálegyenletek megoldása | 341 |
| Rezgéskeltés, veszteségek kiegyenlítése | 346 |
| Utószó | 350 |
| Feladatmegoldások | 351 |
| Tárgymutató | 377 |