Matematika I.

Kézirat/Budapest Műszaki Egyetem Közlekedésmérnöki Kar

Szerző

Dr. Szász Gábor

Budapest

'Dr. Szász Gábor: Matematika I. ' összes példány

Kiadó:	Tankönyvkiadó Vállalat
Kiadás helye:	Budapest
Kiadás éve:	1986
Kötés típusa:	Ragasztott papírkötés
Oldalszám:	458 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	24 cm x 17 cm
ISBN:
Megjegyzés:	A könyv tankönyvi száma: J 7-880. Megjelent 208 példányban. Javított kiadás 4. változatlan kiadása.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Előszó

Ez a jegysorozat négy kötetből áll; mindegyik kötete az 1978-ban életbe lépett közlekedésmérnöki tanterv egy-egy féléves matematika-anyagát foglalja magában. Tartalmaz néhány olyan, a tantárgyi... Tovább

Tartalom

Előszó	3
Bevezetés: A matematika tárgya és módszere	5
A matematika tárgya	5
A fogalmak kialakítása a matematikában	7
Az ítéletek kialakítása a matematikában	9
A matemetikai jelölésmód	11
A matematika kapcsolata a többi tudománnyal és a technikával	11
Halmazelmélet	14
A halmaz fogalma	14
Részhalmaz	16
Műveletek halmazokkal	18
Hatványhalmaz	21
Függvény, leképezés	23
Osztályozás	25
Matematikai logika	26
Ítélet és logikai értéke	26
Logikai műveletek	27
A matematikai logika alapazonosságai	30
Logikai függvények	33
Kvantorok	33
Vektoralgebra	37
A vektor fogalma	37
Vektorok összeadása és kivonása	40
Vektor szorzása számmal	45
Vektorok lineáris kombinációja	48
Vektorrendszer lineáris függetlensége	54
Vektor koordinátái	57
Vektorok skaláris szorzata	61
Másod- és harmadrendű determináns	70
Vektorok vektori szorzata	72
Vektorok vegyes szorzata	78
Analitikus térgeometria	83
Térbeli derékszögű koordináta-rendszer. Geometriai alakzat egyenlete és egyenletrendszere	83
Az egyenes egyenletei és egyenletrendszerei	87
A sík egyenletei	91
Helyzetgeometriai feladatok	94
Méretes feladatok	101
Komplex számok	110
A komplex szám algebrai alakjai	110
Binomiális együtthatók, binomiális tétel	117
A síkbeli polárkoordináta-rendszer	121
A komplex szám trigonometriai alakja	124
Sorozatok	133
A sorozat fogalma	133
Metrikus tér	138
Korlátos halmaz	139
Környezet	142
Sorozat határértéke, konvergencia	144
Műveletek számsorozatokkal	151
Valós számsorozatok konvergenciatételei, végtelenhez divergálása	161
Nevezetes számsorozatok	168
Koordinátákkal adott pontsorozat korlátossága és konvergenciája	177
A Bolzano-Weierstrass-tétel	178
A Cauchy-féle konvergenciakritérium	184
Változó kitevőjű valós számsorozatok	187
Függvényhatárérték és folytonosság	190
Valós függvények megadása	190
Függvény határértéke	197
Függvény folytonossága	208
Egy oldali határérték, egy oldali folytonosság	215
Korlátos zárt halmazon folytonos valós függvények tulajdonságai	219
Érintő és aszimptota	228
Egyváltozós valós függvények és differenciálásuk	237
Differenciálhányados és derivált	237
Magasabb rendű deriváltak	244
A differenciálás általános szabályai	246
Összetett függvények	253
Görbék érintkezése, simulókör	260
Függvény inverze; invertálhatóság és monotonitás	264
Egyváltozós valós elemi függvények és differenciálásuk	273
Elemi függvények	273
Racionális egész függvények	274
Racionális törtfüggvények	281
Páros és páratlan függvények	287
Trigonometrikus függvények; függvény priódusai	289
Logaritmus függvények	297
Exponenciális függvények	303
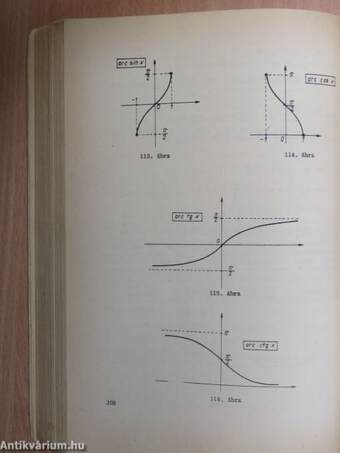
Arkusz függvények	306
Hiperbolikus függvények	315
Area függvények	322
Függvényvizsgálat	329
Függvény szélsőértékei	329
A differenciálszámítás középértéktételei	332
A Taylor-formula	338
Növekedés, csökkenés és szélsőérték meghatározása a deriváltak segítségével	344
Konvexség, konkávság és inflexiós pont meghatározása a deriváltak segítségével	351
L'Hospital-szabály	355
Paraméteresen adott függvény differenciálása	366
Határozatlan integrál	374
Primitív függvény, határozatlan integrál	374
Alapintegrálok	377
Az integrálás általános szabályai	378
Parciális integrálás	382
Integrálás helyettesítéssel	388
Racionális törtfüggvények integrálása	394
Határozott integrál	403
A határozott integrál fogalma	407
A határozott integrál tulajdonságai	411
Folytonos függvények határozott integrálja	418
Improprius integrálok	425
Területszámítás határozott integrállal	430
Térfogatszámítás határozott integrállal	443
Ívhosszúság kiszámítása határozott integrállal	447

Témakörök

Dr. Szász Gábor

Dr. Szász Gábor műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Szász Gábor könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem