Matematika II-III.

Aritmetika és analízis

Szerző

Huszár Géza

Lektor

Dr. Bacskay Zoltán

Dr. Gyires Béla

Budapest

'Huszár Géza: Matematika II-III. ' összes példány

Kiadó:	Tankönyvkiadó Vállalat
Kiadás helye:	Budapest
Kiadás éve:	1959
Kötés típusa:	Ragasztott papírkötés
Oldalszám:	246 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	25 cm x 17 cm
ISBN:
Megjegyzés:	151 fekete-fehér ábrával illusztrálva. Tankönyvi szám: 4167/II-III.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Aritmetika
Elemi aritmetika
A számok oszthatósági viszonyai
Főosztó, főtöbbes, prímszám	7
Euklidesz algoritmusa	8
A főosztó lineáris előállítása	10
Az elsőfokú kétismeretlenes határozatlan egyenlet megoldása	10
Prímtényezős előállítás	12
A főtöbbes kiszámítása	13
Kongruenciák
A kongruencia fogalma	14
Műveletek kongruenciákkal	14
Az Euler-féle függvény	19
Az általánosított Fermat-tétel	21
Közönséges törtek és tizedes törtek	23
Az egy ismeretlenes lineáris maradékegyenlet megoldása	25
Lánctörtek
Véges lánctörtek
A lánctört fogalma	28
A lánctörtek alaptulajdonságai	32
A redukáltak képzési törvénye	35
A redukáltak további vizsgálata	37
Az elsőfokú határozatlan egyenlet megoldása	40
Végtelen lánctörtek
A végtelen lánctört fogalma	42
A lánctörtkifejezés egyértelműsége	44
Szakaszos lánctörtek	46
Lagrange tétele	50
Analízis
Koordinátageometriai bevezetés
Koordinátatranszformáció
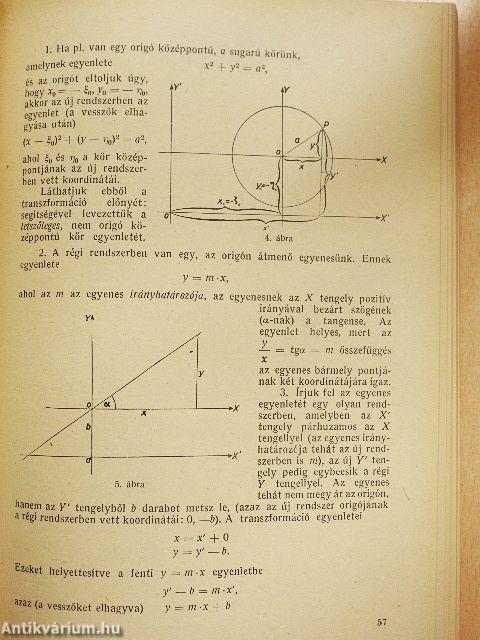
A Descartes-koordináta-rendszer	55
Transzformáció. Eltolás. Egyenes és kör	56
Transzformáció. Elforgatás	59
Transzformáció. Eltolás és elforgatás	63
Első- és másodrendű görbék
Az egyenes normálegyenlete	64
Az ellipszis egyenlete	66
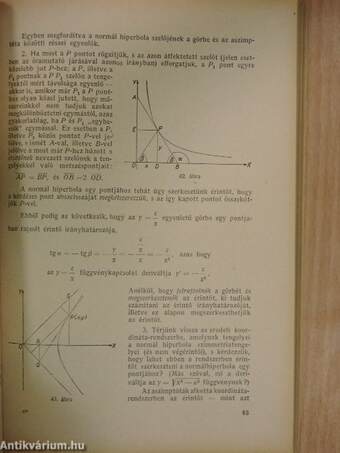
A normál hipberbola egyenlete	68
A hiperbola egyenlete	71
A parabola egyenlete	72
Az algebrai függvénykapcsolatok analízise
A függvényfogalom, az algebrai függvények
Változó és függvény	74
A függvénykapcsolat formája	75
A függvénykapcsolat folytonossága	76
Algebrai alapműveletek a függvénykapcsolatokból	77
A differenciál- és integrálszámítás	79
Az érintőszerkesztés feladata
A kör érintője	80
Az ellipszis érintője	81
A normálhiperbola érintője	82
A hiperbola érintője	84
A parabola érintője	84
Érintőszerkesztés kalkulussal	86
A differenciális kalkulus elemi szabályai
Konstansok szerepe a kalkulusban	80
Összeg, szorzat, és hatvány deriválása	81
Reciprok és hányados deriválása	82
Az összetett függvény és deriválása	84
A törtkitevőjű hatványfüggvény deriválása	84
Az inverz függvény és deriválása	86
Szélsőérték-számítás
A másodfokú függvény szélső értéke kalkulus nélkül	99
Szélsőérték-számítás kalkulussal	101
A görbület	105
Területszámítás
Területszámítás kalkulus nélkül	107
A határozatlan integrál	110
A határozott integrál	114
Az elemi transzcendális függvények analízise
A körfüggvények és inverzeik
Függvénykapcsolatok a körben	116
A körfüggvények és deriválások	117
Az inverz körfüggvények és deriválásuk	123
A körfüggvények és inverzeik a Descartes-rendszerben	126
Az exponenciális függvény
Az exponenciális függvény alaptulajdonságai	129
Az exponenciális függvény deriválása	137
Az organikus növekedés függvénye	137
A logaritmus függvény
Az exponencionális függvény inverze	139
A logaritmusszámítás	139
A logaritmusfüggvény	142
A logaritmusfüggvény deriváltja	143
Transzcendens függvények integrálása
Az elemi transzcendens függvények mint primitív függvények	148
Integrálás helyettesítéssel	146
Paricális integrálás	149
A hiperbolikus függvények	152
Közelítő számítások
Hatványsorok
Bevezető megjegyzések	155
Az exponenciális sor	155
sin x és cos x hatványsora	157
Az általános binomiális függvény sorbafejtése	159
A logaritmusfüggvény és az inverz körfüggvények hatványsora	160
Végtelen sorok
Vég nélkül folytatott műveletek	162
A harmonikus sor	163
A végtelen geometriai sor	165
Az e elhatározása	168
A váltakozó előjelű harmonikus sor	169
Az elemi transzcendens függvények hatványsorának konvergenciája	171
A valószínűségi integrál
A Wallis-formula	172
Integrálok határétéke	174
A valószínűségi integrál	175
Taylor-sor és Taylor-formula
A Taylor-sor	178
A végtelen hatványsorok berekesztése. A maradéktag	181
A Rolle-tétel	182
A Taylor-formula	184
Az interpoláció
Az interpoláció alapelve	188
A Newton-interpoláció	190
A Lagrange-interpoláció	197
Inverz-interpoláció	199
Mechanikus quadratura
Mechanikus quadratura	200
Az ívhossz	204
Kétváltozós függvények
Parciális deriválás
Bevezető megjegyzések	206
Parciális függvények és deriváltak	207
A teljes differenciál	208
Koordináta-rendszerek a térben
A térbeli Descartes-rendszer	211
Térbeli koordinátatranszformáció	212
Poláris koordináta-rendszer	214
Egyenes és sík a térben
Az egyenes a térben	215
Két egyenes hajlásszöge	217
A sík egyenlete	218
A kétváltozós lineáris függvény	219
A másodrendű felületek
A gömb, a forgásellipszoid és a háromtengelyű ellipszoid	220
A kétköpenyű hiperboloid	222
Az elliptikus parabolid	223
Az egyköpenyű hiperboloid és a hiperbolikus parabolid	224
Általánosítások
A teljes differenciál alapképletének geometriai jelentése	225
ATaylor-formula általánosítása	227
A kettős integrál	229
Függelék
Trigonometriai megjegyzések
A trigonometria feladata. A trigonometriai viszonyszámok első definiciója	232
A trigonometriai viszonyszámok második definicója	234
Tompaszögek sinusa és cosinusa	234
A sinustétel	236
A cosinustétel és a Pythagorasz-tétel	238
Ptolemaiosz tétele	239
Hibajegyzék az I. kötethez (kombinatorikához)	241