Matematikai vizsgakövetelmények érettségin, egyetemi és főiskolai felvételin

Fogalmak, ismeretek/Tételek, bizonyítások/Eljárások

Szerző

Lektor

'Horváth János: Matematikai vizsgakövetelmények érettségin, egyetemi és főiskolai felvételin ' összes példány

Kiadó:	Szerzői magánkiadás
Kiadás helye:
Kiadás éve:	1996
Kötés típusa:	Ragasztott papírkötés
Oldalszám:	373 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	20 cm x 14 cm
ISBN:	963-650-388-5
Megjegyzés:	A könyv fekete-fehér ábrákkal illusztrált.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

A halmazelmélet alapjai
Halmazok egyenlősége	17
Részhalmazok	17
Valódi részhalmazok	18
Halmazok számossága	18
Halmazok uniója	19
Halmazok metszete	19
Halmazok különbsége	20
Kiegészítő (komplementer) halmaz	20
Halmazok jelölése	20
Halmazok direkt szorzata	21
A matematikai logika alapjai, fogalmak
Állítás, kijelentés	22
Mi a konjukció	22
Mi a diszjunkció	23
Mi a negáció	23
A számfogalom, fogalmak
A természetes számok	24
Alapműveletek természetes számok körében	24
Osztó	25
Prímszám	25
Relatív prímek	25
Többszörös	26
A számelmélet alaptétele	26
A legnagyobb közös osztó	26
A legkisebb közös többszörös	27
A számfogalom kiterjesztésének szükségessége	27
A permanencia elve	28
A negatív számok	28
Az egész számok halmaza	29
A racionális számok halmaza	29
Az irracionális számok halmaza	30
Az irracionális számok tizedestört alakja	30
A valós számok halmaza	31
A valós számok és a számegyenes	31
Összadás és szorzás a valós számkörben	32
A tizes számrendszer	32
A kettes számrendszer	33
A számok abszolútértéke	33
A számok normálalakja	34
Algebra, fogalmak
Azonosság	34
Az egyenlet	34
Az egyenlőtlenség	35
Logikai függvény	35
Az egyenletek ekvivelanciája	35
Ekvivalens átalakítások	36
A hamis gyök	37
A gyökvesztés	37
A polinom	37
Az algebrai tört	38
A másodfokú egyenlet diszkriminánsa	38
A másodfokú egyenlet gyöktényezős alakja	38
A hatványfogalom egész kitevőkre	39
A négyzetgyök	39
Az n-edik gyök	40
A racionális kitevőjű hatványok	40
A számok számtani közepe	41
A számok mértani közepe	41
A logarimus	42
Az exponenciális egyenlet	42
A logaritmikus egyenlet	43
Függvények, fogalmak
A függvény fogalma, megadásának módjai	43
Az értelmezési tartomány	44
Az értékkészlet	44
Az egyértelmű leképzés	45
Kölcsönös egyértelmű leképezés	45
Monoton növekedés	46
Monoton fogyás	46
A függvény páratlansága	47
A függvény párossága	47
Szélsőérték, szélsőértékhely	48
A függvény zérushelye	48
A függvény korlátossága	49
Periodikusság	49
Inverz függvények	50
Az inverz függvény ábrázolása	50
Konstans függvény	51
Az egyenes arányosság	51
A fordított arányosság	52
Az elsőfokú függvények	52
Az abszolútérték függények	53
A másodfokú függvények	53
A sinus függvény	54
A cosinus függvény	55
A tangens függvény	56
A cotangens függvény	57
Az exponenciális függvény	58
A logaritmikus függvény	58
A négyzetgyök függvény	59
A számsorozat	59
A számtani sorozat	60
A mértani sorozat	60
A mértani sor	61
Elemi geometria, fogalmak
Szögfelező a síkban és a térben	61
A szakaszfelező merőleges és sík	62
Kör, körvonal, körlap	62
Gömb, gömbfelület, gömtest	63
Látószögalakzat	63
Thalész-kör	64
A parabola	64
Az ellipszis	65
A hiperbola	65
A transzformációk, mint függvények	66
A transzformációk invariáns és fix alakzatai	66
Tükrözés egyenesre	67
Tükrözés síkra	67
A tengelyes szimmetria	68
A középpontos tükrözés	68
Az eltolás	69
A pont körüli elforgatás	69
Az egyenes körüli elforgatás	70
Két síkidom egybevágósága	70
Tengelyesen szimmetrikus alakzatok	71
Síkszimmetrikus testek	72
Egybevágósági transzformációk	72
Középpontosan szimmetrikus alakzatok	72
A háromszög oldalfelező merőlegesei	73
A háromszög szögfelezői	73
A háromszög magasságvonalai és magasságpontja	74
A háromszög súlyvonalai és súlypontja	74
A háromszög nevezetes körei	75
A szög ívmértéke	75
A kör érintője	76
A parabola érintője	76
A középponti szögek	77
A kerületi szögek	77
Látószögek	78
A paralelogramma	78
A rombusz	79
A négyzet	79
A téglalap	79
A deltoid	80
A trapéz	80
A középvonalak	81
Érintőnégyszögek	81
Húrnégyszögek	81
A síknégyszögek osztályozása	82
Szabályos sokszögek	83
Hasáb	83
Henger	84
Paraleleipedon	84
Téglatest	85
Kocka	85
Négyzetes oszlop	85
Kúp	86
Gúla	86
Csonkagúla	87
Csonkakúp	87
Középpontos hasonlóság és tulajdonságai	88
Hasonlóság	88
A háromszögek egybevágóságának alapesetei	89
A háromszögek hasonlóságának alapesetei	89
Térelemek és kölcsönös helyzetük	90
A tétel és megfordítása	90
Pont és egyenes távolsága	91
Pont és sík távolsága	91
Párhuzamos egyenesek távolsága	92
Párhuzamos síkok távolsága	92
Kitérő egyenesek távolsága	93
Kitérő egyenesek hajlásszöge	93
Egyenes és sík hajlásszöge	94
Két sík hajlásszöge	94
Geometriai számítások, fogalmak
A vektor, vektorok egyenlősége	95
Bázisvektorok, a vektorok koordinátái	95
Egységvektor, helyvektor	96
A vektor koordinátái	96
Vektorok összeadása	97
Vektorok különbsége	97
Vektor szorzása skalárral, tulajdonságai	98
A vektor abszolútértéke	98
Két vektor skalárszorzata, ez mikor 0?	99
A terület fogalma	99
A térfogat fogalma	100
A körcikk területe	100
A körszelet területe	101
A vonal egyenlete	101
Az egyenes iránytangense	101
Hegyesszögek szögfüggvényei	102
Tetszőleges szög sinusa és cosinusa	103
Tetszőleges szög tangense és cotangense	104
A halmazelmélet alapjai, tételek és bizonyítások
A halmazok úniója kommutatív	107
A halmazok úniója asszociatív	108
A halmazok metszetképzése kommutatív	109
A halmazok metszetképzése asszociatív	110
A matematikai logika alapjai
A konjunkció kommutatív művelet	115
A konjunkció asszociatív művelet	116
A diszjunkció kommutatív művelet	117
A diszjunkció asszociatív művelet	118
A konjunkció negációja	119
A számfogalom, tételek és bizonyítások
A racionális számok tizedestört alakja	111
A gyökvonás kivezet a racionális számok halmazából	112
Algebra, tételek és bizonyítások
Két tag négyzetének különbsége	113
Szorzat hatványa	114
A tört hatványa	115
Hatvány hatványa	116
Egyenlő alapú hatványok szorzata	117
Egyenlő alapú hatványok hányadosa	118
A szorzat négyzetgyöke	119
A hányados négyzetgyöke	120
A szorzat n-edik gyöke	121
A hányados n-edik gyöke	122
Az n-edik gyök hatványa	123
A másodfokú egyenlet megoldóképlete	124
A másodfokú egyenlet gyöktényezős alakja	126
Gyökök és együtthatók közti összefüggések	127
A számtani és mértani közép összehasonlítása	128
A szorzat logaritmusa	130
A hányados logaritmusa	131
A hatvány logaritmusa	132
Áttérés más alapú logaritmusra	133
Függvények, tételek és bizonyítások
A számtani sorozat n-edik eleme	134
A számtani sorozat első n tagjának összege	135
A mértani sorozat n-edik eleme	136
A mértani sorozat első n elemének összege	137
Az első n négyzetszám összege	138
A mértani sor q kisebb mint 1 esetén konvergens	139
Elemi geometria, tételek és bizonyítások
A háromszög belső szögeinek összege	140
A háromszög külső szögeinek összege	141
A sokszög belső és külső szögeinek összege	142
A háromszög oldala és szemközti szöge	143
A mellékszögek szögfelezői	144
A háromszög belső szögfelezői	145
A háromszög oldalfelező merőlegesei	146
A háromszög magasságvonalai	147
A háromszög súlyvonalai	148
Thalész tétel	149
Az érintőnégyszög tétele	151
Az érintőnégyszög tétel megfordítása	152
A húrnégyszög tétele	154
A húrnégyszög tétel megfordítása	155
A paralelogramma középpontosan szimmetrikus	156
A paralelogramma középvonala	158
A háromszög középvonala	159
A trapéz középvonala	160
A középponti szögek és a körív aránya	161
A középponti szögek és a körcikk területe	162
A középponti és kerületi szögek tétele	164
A látószög tétele	163
A háromszögek egybevágóságának alapesetei	166
A párhuzamos szelők tétele	168
A párhuzamos szelők tételének megfordítása	169
A középpontos hasonlóság tulajdonságai	170
A háromszögek hasonlóságának alapesetei	172
A négyszögek hasonlósága	174
A gúla alappal párhuzamos síkmetszetei	175
Befogótételek	177
A magasságtétel	178
A kör érintője és szelőjére vonatkozó tétel	179
A háromszög belső szögfelezője és a metszett oldal (szögfelezőtétel)	171
Pitagorasz tétele	180
Pitagorasz tételének megfordítása	181
Geometriai számítások, tételek és bizonyítások
A vektorösszeg harmadikkal való szorzása	182
A vektorműveletek koordinátákkal	183
A skalárszorzat mikor nulla?	184
Két vektor skalárszorzatának koordinátái	185
Vektorösszeg számmal szorzása disztributív	186
A pótszöges összefüggések	188
Szögfüggvények pitagoraszi összefüggése	189
A negatív szögek szögfüggvényei	190
A háromszög trigonometrikus területképletei	187
A síkidom merőleges vetületének területe	150
A háromszög köré írt kör sugara, oldala és szemközti szöge közti összefüggés	191
A szinusz tétel	192
A koszinusz tétel	193
Addíciós tételek	195
A sin alfa plusz-mínusz béta	196
A sin alfa plusz-mínusz béta és cos alfa plusz-mínusz béta	197
A tg alfa plusz-mínusz béta	198
Kétszeres szögek szögfüggvényei	199
A hasonló háromszögek és sokszögek területének aránya	200
A hasonló gúlák térfogatának aránya	176
A hasáb térfogata	201
A henger térfogata	203
A gúla térfogata	204
A kúp térfogata	206
A csonkagúla térfogata	207
A csonkakúp felszíne	208
A csonkakúp térfogata	209
A gömb térfogata	210
A gömb felszíne	211
Két pont távolsága koordinátáiból	212
A szakasz felezőpontjának koordinátái	213
A szakasz harmadolópontjainak koordinátái	214
A háromszög súlypontjának koordinátái	215
A szakasz osztópontjainak koordinátái	216
Az egyenes irányvektoros egyenlete	217
Az egyenes normálvektoros egyenlete	218
Az egyenes iránytényezős egyenlete	219
Az egyenes és a kétismeretlenes elsőfokú egyenlet	220
Vektorok párhuzamossága és merőleges vektorok	221
Az egyenes párhuzamosságának és merőlegességének feltétele	222
A kör egyenlete	223
A kör és a kétismeretlenes másodfokú egyenlet	224
A parabola csúcsponti egyenlete	225
A parabola és a kétismeretlenes másodfokú egyenlet	227
Az ellipszis középponti egyenlete	228
A hiperbola középponti egyenlete	229
A matematikai logika alapjai, tételek és bizonyítások
A konjunkció művelet kommutatív	230
A konjunkció asszociatív művelet	229
A diszjunkció művelek kommutatív	232
A diszjunkció művelet asszociatív	233
A konjunkció negációja	234
A halmazelmélet alapjai, eljárások
Halmazok ábázolása Venn diagrammon	237
Teljes indukció	238
Halmazok megadása különféle jelölésekkel	239
Véges halmaz részhalmazainak száma	240
A számfogalom, eljárások
Természetes számok felbontása prímtényezőkre	241
A számok felírása kettes számrendszerben	242
A számok legnagyobb közös osztójának kiszámítása	243
A számok legkisebb közös többszörösének kiszámítása	244
Algebra, eljárások
Műveletek egész kifejezésekkel	245
Műveletek törtkifejezésekkel	246
Törtkifejezések értelmezési tartományának meghatározása	247
Négyzetgyökös kifejezések értelmezési tartományának meghatározása	248
A logaritmikus kifejezések értelmezési tartományának meghatározása	249
A lineáris egyenletek grafikus megoldása	250
A lineáris egyenletek algebrai megoldása	251
A lineáris egyenlőtlenségek grafikus megoldása	252
A lineáris egyenlőtlenségek algebrai megoldása	254
A lineáris kétismeretlenes egyenletrendszerek grafikus megoldása	255
A lineáris kétismeretlenes egyenletrendszerek algebrai megoldása	256
A másodfokú egyenletek megoldása	257
A másodfokúra vezető egyenletek megoldása	258
Törtes egyenletre vezető szöveges feladatok	259
Egyenletrendszerre vezető szöveges feladatok	260
Másodfokú egyenletre vezető szöveges feladatok	261
Törtes egyenlőtlenségek megoldása	262
Négyzetgyökös egyenletek megoldása	263
Exponcenciális egyenletek megoldása	264
Logaritmikus egyenletek megoldása	265
Abszolútértékes egyenletek megoldása	266
A nevező gyöktelenítése	268
Kivitel a gyökjel alól és bevitel a gyökjel alá	269
Számok n-edik gyökének kiszámítása	270
Számok normálalakjának felírása	271
Függvények, eljárások
Függvények ábrázolása derékszögű koordinátarendszerben	272
Az abszolútérték függvény ábrázolása és jellemzése	273
A négyzetgyök függvény ábrázolása és jellemzése	274
A másodfokú függvények transzformálása	275
A másodfokú egyenletek grafikus megoldása	276
A másodfokú egyenlőtlenségek grafikus megoldása	278
Szélsőérték feladatok megoldása másodfokú fügvényekkel	279
A szinusz függvény ábrázolása és jellemzése	280
A koszinusz függvény ábrázolása és jellemzése	281
A tangens függvény ábrázolása és jellemzése	282
A kotangens függvény ábrázolása és jellemzése	283
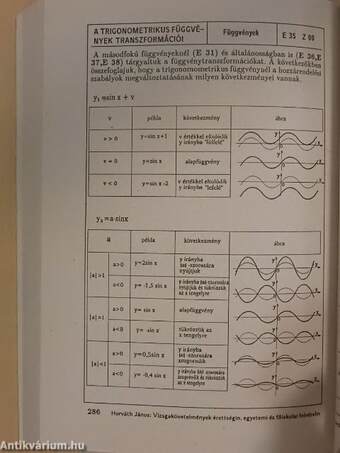
Trigonometrikus függvények transzformációi	286
Függvénytranszformációk: x és y irányú eltolás	284
Függvénytranszformációk: x és y irányú tükrözések	285
Függvénytranszformációk: x és y irányú nyújtások	288
A transzformációk egymásutánja	289
Az exponenciális függvény ábrázolása és jellemzése	290
A logaritmikus függvény ábrázolása és jellemzése	291
Elemi geometria, eljárások
A parabola ponjainak szerkesztése	292
Az ellipszis ponjainak szerkesztése	293
A hiperbola ponjainak szerkesztése	294
A számhalmazok ábrázolása számegyenesen	295
A ponthalmazok jellemzése a síkon, rendezett számpárokkal	296
A tengelyes tükrözés végrehajtása	297
A középpontos tükrözés végrehajtása	299
Az eltolás végrehajtása	300
Az elforgatás végrehajtása	301
Külső pontból körhöz érintő szerkesztése	302
Két kör közös külső érintőinek szerkesztése	303
Két kör közös belső érintőinek szerkesztése	305
Középpontos nagyítás és kicsinyítés	307
Szakasz adott arányú felbontása	308
Adott szöghöz látókörív szerkesztése	309
Diszkusszió	310
Geometriai számítások, eljárások
Vektorok felbontása összetevőkre	311
A vektor abszolútértéke koordinátáiból	312
Hogyan mérünk szöget?	313
Nevezetes szögek szögfüggvényértékei	315
Nevezetes szögek szögfüggvényértékeinek táblázata	316
Trigonometrikus egyenletek megoldása	318
A derékszögű háromszög trigonometriája	314
Az általános háromszög trigonometriája	320
A háromszög területének kiszámítása	321
A négyszög területének kiszámítása	322
A sokszög területének kiszámítása	323
A kör részeinek területe	325
A hasáb térfogatának és felszínének kiszámítása	327
A henger térfogatának és felszínének kiszámítása	329
A gúla térfogatának és felszínének kiszámítása	330
A forgáskúp térfogatának és felszínének kiszámítása	331
A csonkagúla térfogatának és felszínének kiszámítása	332
A csonkakúp térfogatának és felszínének kiszámítása	333
A gömb térfogatának és felszínének kiszámítása	334
Az egyenes egyenlete két pontja alapján	335
Az egyenes egyenlete adott pontja és irányvektora alapján	336
Az egyenes egyenlete adott pontja és irányszöge alapján	337
Az egyenes egyenlete adott pontja és normálvektora alapján	338
Az egyenes jellemzői az egyenlete alapján	339
Az egyenesek metszéspontja	340
A kör egyenletének felírása	341
A kör és egyenes metszéspontjának kiszámítása	342
Két kör metszéspontjának kiszámítása	344
A kört érintő egyenes egyenlete	345
A kör adatai az egyenletéből	346
A parabola adatai az egyenletéből	347
A parabolát érintő egyenes egyenlete	348
Tárgymutató	349
Útmutató első gimnazistáknak	362
Útmutató másodikos gimnazistáknak	363
Útmutató harmadikos gimnazistáknak	364
Útmutató negyedikes gimnazistáknak	365
Útmutató elsős szakközépiskolásoknak	366
Útmutató másodikos szakközépiskolásoknak	367
Útmutató harmadikos szakközépiskolásoknak	368
Útmutató negyedikes szakközépiskolásoknak	369
Tartalomjegyzék A "zöld könyv" szerinti sorrendben	370

Témakörök

Horváth János

Horváth János műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Horváth János könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem