A gépi matematika numerikus módszerei

Analízis, algebra, optimalizálás, közönséges differenciálegyenletek

Szerző

Fordító

Grafikus

Lektor

Budapest

'N. Sz. Bahvalov: A gépi matematika numerikus módszerei ' összes példány

Kiadó:	Műszaki Könyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1977
Kötés típusa:	Vászon
Oldalszám:	551 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	24 cm x 17 cm
ISBN:	963-10-1753-2
Megjegyzés:	62 fekete-fehér ábrával illusztrált. Tankönyvi szám: 60726.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Előszó	9
Bevezetés	11
A matematikai analízis numerikus módszerei
A numerikus megoldás hibája	19
A hibák forrásai és osztályozásuk	19
Számábrázolás az elektronikus számítógépben	21
Abszolút és relatív hiba. Adatfelírási formák	22
A számítási hiba	24
A függvény hibája	25
Az interpoláció és azzal kapcsolatos kérdések	31
Az approximációs feladat kitűzése	32
A Lagrange-féle interpolációs polinom	35
A Lagrange-féle interpolációs polinom maradéktagjának becslése	36
Osztott defferenciák és tulajdonságaik	37
A Newton-féle interpolációs formula előállítása osztott differenciákkal	39
Osztott differenciák és interpolálás ismétlődő alappontokon	41
Végesdifferencia-egyenletek	46
A Csebisev-féle polinomok	54
Az interpolációs formula maradéktagbecslésének minimalizálása	57
Véges differenciák	60
Ekvidisztans alappontú Newton-féle interpolációs formula	63
Bessel-féle és Everett-féle interpolációs formulák. Táblázatok készítése	65
Az interpolálás kerekítési hibái	72
Az interpolációs módszerek használata. Inverz interpoláció	74
Ortogonális rendszerek és tulajdonságaik	75
Ortogonális polinomok	80
Numerikus differenciálás	83
A numerikus differenciálás képleteinek számítási hibája	87
Közelítő integrálás	89
Newton-Cotes-féle kvadraturaképletek	89
Kvadraturaképletek hibabecslése függvényosztályokra	96
Gauss-féle kvadraturaképletek	100
Az elemi kvadraturaképletek gyakorlati hibabecsléséről	100
Erősen oszcilláló függvények integrálása	115
Az integrálás pontosságának növelése a szakasz egyenlő részekre osztásának segítségével	118
Az optimalizálási feladat kitűzései	122
Optimális kvadraturák az egyszer differenciálható függvények osztályán	126
A kvadraturaképlet osztópontjai eloszlásának optimalizálása	132
Példák az osztópontok optimális kiválasztására	138
A hiba főtagja	143
Az Euler- és a Gregory-formula	147
A Runge-szabály a hiba gyakorlati becslésére	150
A Romberg-formulák	156
Mérési adatok és azok kiértékelése	159
Integrálok kiszámítása nemreguláris esetben	165
Automatikus lépéshosszválasztással működő könyvtári programok felépítési elvei	171
Numerikus integrálás könyvtári programjai	177
Approximáció és ahhoz kapcsolódó kérdések	184
Legjobb közelítés a lineáris nomált térben	184
Legjobb közelítés a Hilbert-térben, és a gyakorlati előállítás során felmerülő kérdések	186
Diszkrét Fourier-transzformáció	191
Gyors Fourier-transzformáció	194
Az egyenletesen legjobb közelítés	196
Példák egyenletesen legjobb közelítésre	199
Iterációs módszer egyenletesen legjobban közelítő polinom előállítására	205
Polinomok felírási módjai	210
Elemi függvények kiszámítási módjai	216
Különböző függvényosztályok közelítésének sebessége	220
Interpoláció és közelítés spline-okkal	222
Entrópia és e-entrópia	228
Többdimenziós feladatok	234
A határozatlan együtthatók módszere	235
A legkisebb négyzetek módszere	236
A regularizálás módszere	238
Példa regularizálásra	236
Többdimenziós feladatok visszavezetése egydimenziósra	244
A numerikus integrálás hibabecslése egyenlete rácson	251
A numerikus integrálás hibájának alsó becslése	253
A hibabecslés optimalizálása az integrálási módszerek bővebb osztályain	256
A Monte-Carlo-módszer	259
A feladatmegoldás nemdeterminisztikus módszereinek indokoltsága	246
A Monte-Carlo-módszer konvergenciájának gyorsítása	266
Nagyobb pontosságú kvadraturaképletek véletlen osztópontokkal	269
A feladatmegoldási módszer kiválasztása	273
Algebrai és optimalizálási feladatok
Az algebra numerikus módszerei	281
Az eliminációs módszer	282
Az ortogonalizáiós módszer	289
Az egyszerű iterációs módszer	291
A ténylegesen lejátszódó iterációs eljárás vizsgálata	296
Mátrixsereg spektruma	299
A sigmanégyzet-eljárás a gyakorlati hibabecslésre és a konvergencia gyorsítására	304
Az iterációs eljárások kongergenciasebességének optimalizálása	306
A Seidel-módszer	316
A legmeredekebb csökkenés módszere (gradiensmódszer)	321
A konjugált gradiensmódszer	324
Lineáris egyenletrendszerek megoldása a Monte-Carlo-módszerrel	329
Spektrálisan ekvivalens operátorokat felhasználó iterációs módszerek	335
Az egyenletrendszerek közelítő megoldásának hibája és a mátrixok kondicionáltsága. Regularizálás	338
A sajátérték-probléma	343
A teljes sajátérték-probléma megoldása szimmetrikus mátrix esetén forgatási módszerrel	348
A nemlineáris egyenletrendszerek és az optimalizálási feladatok megoldása	352
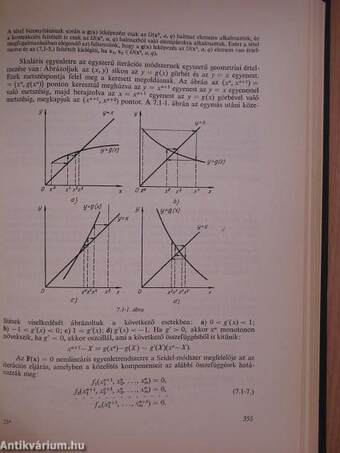
Az egyszerű iterációs módszer és az ehhez kapcsolódó kérdések	353
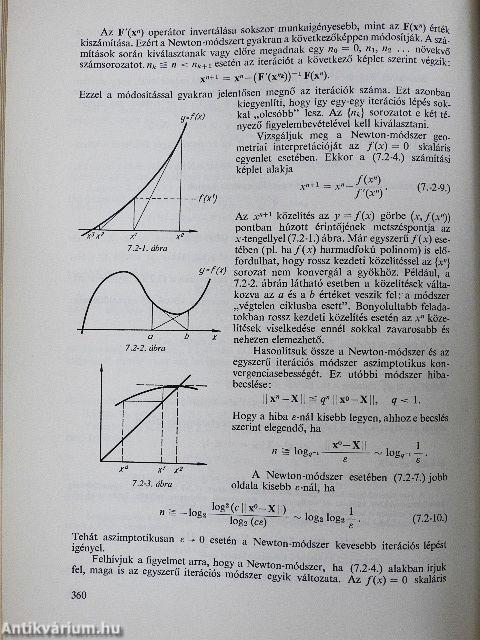
Newton-módszer nemlineáris egyenletek megoldására	357
Más módszerek egyismeretlenes egyenletek megoldására	361
Az iránymenti csökkentés módszere	365
Többdimenziós feladatokat alacsonyabb dimenziós feladatokra visszavezető más módszerek	369
Stacionárius feladatok megoldása stabilizálással	372
Mit optimalizáljunk?	377
Hogyan optimalizáljunk?	381
Közönséges differenciálegyenletek numerikus megoldása
A Cauchy-feladat numerikus megoldása	389
A megoldás Taylor-sorba fejtése	390
Runge-Kutta-módszerek	391
Módszerek lépésenkénti hibaellenőrzéssel	399
Egylépéses módszerek hibabecslése	400
Végesdifferencia-módszerek	405
A határozatlan együtthatók módszere	409
A végesdifferencia-módszerek tulajdonságainak vizsgálata modellfeladatokon	413
A végesdifferencia-módszerek hibabecslése	419
A hiba főtagja	419
A végesdifferencia-módszerek hibabecslése	419
A hiba főtagja	424
A végesdifferencia-módszerek tulajdonságainak vizsgálata pontosabb modelleken	428
Egyenletrendszerek integrálása	436
Általános kérdések	445
Másodrendű egyenletek numerikus integrálási képletei	451
A Cauchy-feladat numerikus megoldásának hibabecslése másodrendű egyenletekre	454
Kétoldali becslési módszerek	459
Közönséges differenciálegyenletek peremértékfeladatainak numerikus megoldási módszerei	465
Másodrendű egyenletek peremérték-feladatainak legegyszerűbb megoldási módszerei	465
A differenciaegyenet peremérték-feladatának Green-függvénye	471
A legegyszerűbb differenciaegyenlet peremérték-feladatának megoldása	476
A numerikus lineáris rendszerek peremérték-feladatainak elemzése	492
Az elsőrendű egyeletrendszerek peremérték-feladatainak megoldási algoritmusai	496
A differenciális ortogonális faktorizációs módszerei	502
Nemlineáris peremérték-feladatok	507
Speciális típusú approximációk	515
Végesdifferencia-módszerek sajátértékek keresésére	522
A számítási hiba hatása a végesdifferencia-egyenlet felírási módjától függően	532
A számítási hiba becslése a peremérték-feladat faktorizációs módszerrel való megoldás esetében	537
Irodalom	541
Tárgymutató	547

Témakörök

N. Sz. Bahvalov

N. Sz. Bahvalov műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: N. Sz. Bahvalov könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem