Nemeuklideszi geometriák elemei

A Bolyai-Lobacsevszkij-féle hiperbolikus geometria és a Riemann-féle (egyszeres és kétszeres) elliptikus geometria vázlatos ismertetése

Szerző

Szerkesztő

Grafikus

Lektor

Budapest

'Kálmán Attila: Nemeuklideszi geometriák elemei ' összes példány

Kiadó:	Tankönyvkiadó Vállalat
Kiadás helye:	Budapest
Kiadás éve:	1989
Kötés típusa:	Ragasztott papírkötés
Oldalszám:	311 oldal
Sorozatcím:	Ifjú matematikusok könyvtára
Kötetszám:	1
Nyelv:	Magyar
Méret:	20 cm x 14 cm
ISBN:	963-181-550-1
Megjegyzés:	Tankönyvi szám: 29291. 288 fekete-fehér ábrával illusztrált.

Értesítőt kérek a kiadóról

Értesítőt kérek a sorozatról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Előszó

A tízes számrendszert az érti igazán, aki ismer más alapú számrendszereket is. Az iskolában tanult euklideszi geometriáról is teljesebb, pontosabb képet kapunk, ha bepillantunk egyéb geometriai... Tovább

Tartalom

Előszó	9
Hivatkozások; jelölések	11
Előkészítés	13
A matematikai pontosságról	13
A szemünknek higgyünk inkább vagy a logikánknak?	14
A matematikai tér nem azonos a fizikai térrel	17
Tételláncok; axiómák	17
Fogalomláncok; alapfogalmak	19
Az axiómarendszerekről általában	22
EUKLIDÉSZ Elemek című munkája és előzményei	23
EUKLIDÉSZ definíciói; posztulátumai; axiómái	26
EUKLIDÉSZ definícióiból	26
EUKLIDÉSZ posztulátumai	26
EUKLIDÉSZ axiómái	27
HILBERT axiómarendszere	27
Illeszkedési axiómák	28
Rendezési axiómák	29
Egybevágósági axiómák	31
Folytonossági axiómák	33
Párhuzamossági axióma	36
Abszolút (vagy neutrális) geometria	37
A maradék axiómarendszer és az abszolút (vagy neutrális) geometria elnevezés magyarázata	37
A párhuzamossági axióma különféle alakjai (helyettes axiómák)	37
Néhány helyettes axióma	38
Néhány abszolút geometriai tétel	40
A helyettes axiómák egyenértékűsége	44
Biztató próbálkozások EUKLIDÉSZ "szégyenfolt"-jának eltüntetésére (SACCHERI és LAMBERT)	57
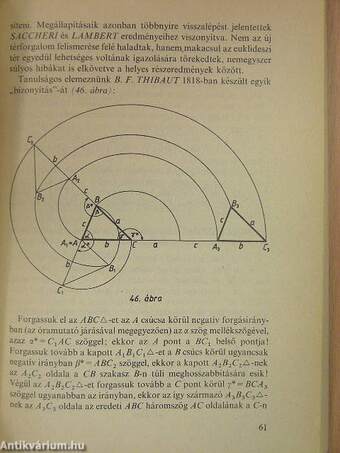
Megtorpanások és helyes részeredmények (THIBAUT; LEGENDRE; SCHWEIKART; TAURINUS)	60
Még néhány abszolút geometriai tétel	67
Feladatok az abszolút geometriából	79
BOLYAI-LOBACSEVSZKIJ-féle hiperbolikus geometria
Amit már az eddigi ismereteink alapján is tudunk az "új geometriá"-ról	83
Mozaikok BOLYAI JÁNOS életéből	86
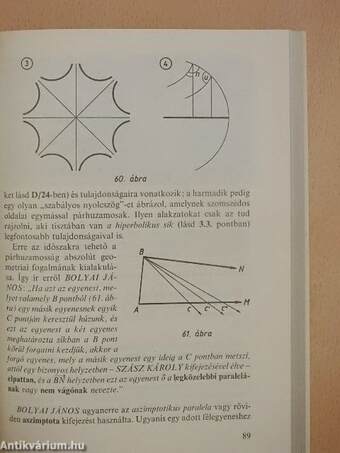
A párhuzamosság értelmezése	94
BOLYAI JÁNOS A tér abszolút igaz tudománya (Appendix) című művének vázlatos ismertetése	103
A párhuzamosság	105
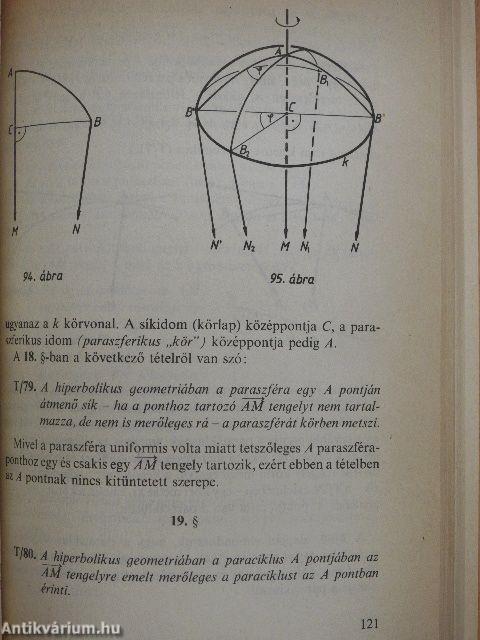
A paraciklus és a paraszféra	113
Trigonometria	136
Az analízis módszereinek alkalmazása; a geometria és a valóság viszonya	151
Szerkesztések	152
GAUSS elmélkedésének eredményeiről	160
LOBACSEVKSZKIJ geometriai vizsgálatairól	166
A hiperbolikus geometria további útjáról	181
A CAYLEY-KLEIN-modell	184
A hiperbolikus geometria ellentmondásmentességéről	195
Feladatok a hiperbolikus geometria köréből	197
A gömbi és az elliptikus geometriákról	201
Létezhet-e az euklideszi és a BOLYAI-LOBACSEVSZKIJ-geometrián kívül más abszolút (neutrális) geometria?	201
A felületelmélet elemei	206
A szférikus (gömbi) geometriáról	210
A projektív sík és a gömbfelület egy lehetséges kapcsolata	222
Kétféle elliptikus geometria értelmezése (RIEMANN)	227
Az elliptikus geometriák további tulajdonságairól	232
Az egyenes és a háromszög	235
A pólus és a poláris	238
A háromszög területe	245
A kör	247
A projektív sík és az elliptikus sík kapcsolata	252
Tájékozódás az egyszeres elliptikus síkon	254
Többféle geometria együtt	257
Az euklideszi, a BOLYAI-LOBACSEVSZKIJ-féle hiperbolikus és a RIEMANN-féle elliptikus geometriák néhány fontos tulajdonságának összehasonlítása	288
Melyik geometria írja le a legpontosabban a fizikai világot?	289
Útmutatások a feladatok megoldásához	293
Utószó	305
Irodalomjegyzék	306
Tárgymutató	309

Témakörök

Kálmán Attila

Kálmán Attila műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Kálmán Attila könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem