Numerikus módszerek I.

Elmélet-Gyakorlat-Szoftver

Szerző

Stoyan Gisbert

Takó Galina

Lektor

Gyurkovics Éva

Budapest

'Stoyan Gisbert: Numerikus módszerek I. ' összes példány

Kiadó:	ELTE-TypoTEX
Kiadás helye:	Budapest
Kiadás éve:	1993
Kötés típusa:	Ragasztott papírkötés
Oldalszám:	388 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	24 cm x 17 cm
ISBN:	963-7546-31-6
Megjegyzés:	Floppy-lemez nélkül. Fekete-fehér ábrákkal.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

A gépi számítás jellegzetességei	13
Az egész számok	13
A lebegőpontos számok	14
Lebegőpontos számítás, kerekítés	15
Kondíciószámok, stabilitás, kerekítés	18
Hibák, kondíciószámok, algoritmusok, stabilitás	18
A kivonás hibaanalízise	21
A numerikus differenciálás	21
Másodfokú egyenletek gyökeinek kiszámítása	23
Skalárszorzatok hibája	24
Determinánsok kiszámítása	26
Lineáris regresszió	26
A számítógépek felépítéséről és a párhuzamos számításról	27
Összefoglalás	29
Feladatok	29
Lineáris egyenletrendszerek	31
Lineáris rendszerek eredete	31
Normák, kondíciószámok, becslések	34
Gauss-elimináció és LU-felbontás	42
A Gauss-elimináció	42
A Schur-féle komplementer	44
A Gauss-elimináció és az LU-felbontás viszonya	47
Domináns főátlójú mátrixok, M-mátrixok	50
Algoritmusok, műveletigény	54
Az LU-felbontás általános mátrixokra: főelemkiválasztás	57
Az LU-felbontás stabilitása, hibaanalízise	60
Direkt módszerek szimmetrikus mátrixokra	65
Ritka mátrixok	69
A Gauss-Jordan algoritmus	76
Összefoglalás	77
Feladatok	78
Lineáris egyenletrendszerek iterációs megoldása	82
Iterációs vagy direkt módszer?	82
Iterációs módszerek konvergenciája	84
Alapvető stacionárius iterációs eljárások	91
A Gauss-Seidel iteráció változatai	97
Az inkomplett LU-felbontás	107
Az egyszerű iteráció; prekondicionálás	110
A Csebisev-iteráció	113
A konjugált gradiens módszer	119
Összefoglalás	130
Feladatok	130
A legkisebb négyzetek feladata	134
Bevezetés	134
Legjobb közelítés anach- és Hilbert-terekben	136
A Gauss-féle normálegyenletek	143
Ortogonálizációs eljárások, QR-felbontás	145
A Houscholder-féle QR-felbontás	147
A szinguláris felbontás	151
A többértelműen megoldható legkisebb négyzetek feladata	151
A szinguláris felbontás létezése, struktúrája	152
Az általánosított inverz mátrix	154
További megoldási módszerek a legkisebb négyzetek feladatára	158
Szekvenciális és párhuzamos feldolgozás	158
A Givens-eljárás	160
Iterációs módszerek	163
Összefoglalás	167
Feladatok	168
Sajátérték feladatok	174
Sajátérték feladatok eredete	174
Stabilitási problémák	174
Rezgési és rezonancia problémák	175
Elméleti tudnivalók	176
A sajátértékek és sajátvektorok alapvető tulajdonságai	176
A karakterisztikus polinomról	178
A sajátértékek lokalizációja	179
Becslések	181
A Jacobi-módszer	184
Leírás, konvergencia	184
Gyakorlati szempontok	186
Vektoriterációk	187
A hatványmódszer	187
Az inverz iteráció	190
A Houscholder-eljárás	192
QR-módszer és változatai; felezési algoritmus	195
QR-módszer	195
A felezési módszer	198
További sajátérték feladatok	200
Általánosabb stabilitási problémákról	200
Az általnosított sajátérték feladat	200
Markov-láncok	201
Összefoglalás	203
Feladatok	203
Interpoláció, approximáció	209
Interpolációs feladatok keletkezéséről	209
Lagrange-interpoláció	211
Folytonos függvények approximációja Bernstein-polinommal	220
A Hermite-féle interpoláció	225
Spline interpoláció	227
Négyzetes polinomiális közelítések	239
Trigonometrikus interpoláció, gyors Fourier-transzformáció	246
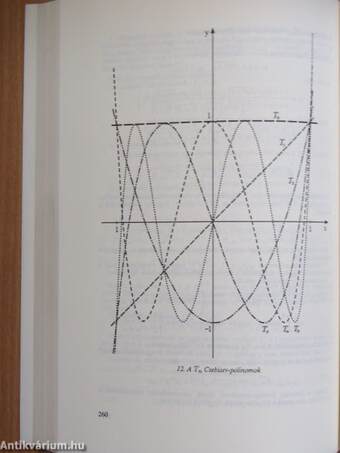
Ortogonális polinomok	254
Egyenletesen legjobb közelítés	264
Többdimenziós interpoláció	269
Sík- és térgörbék interpolációja	269
Tenzorszorzat interpoláció	272
Szabálytalanul elhelyezkedő alappontok	273
Összefoglalás	276
Feladatok	277
Közelítő integrálás	286
Motiváció	286
Elemi kvadratúra képletek	287
Kvadratúra képletek konvergenciája	288
Interpolációs kvadratúra képletek	292
Összetett kvadratúra képletek	295
A Romberg-integráció	297
Gyakorlati szempontok	301
Gauss-integráció	303
Speciális integrandusok kezelése	308
Lobatto- és Kronrod-integráció	310
Többdimenziós integrálok kiszámítása	311
Összefoglalás	316
Feladatok	316
Nemlineáris egyenletek, egyenletrendszerek és szélsőérték feladatok	322
Motiváció	322
Felezési módszer, egyszerű iterációk	324
A Newton-módszer és változatai	326
Leírás, konvergencia	326
Konvergenciarend, lokális konvergencia	328
A Newton-módszer változatai; gyakorlati szempontok	329
Monoton konvergencia	334
Egyenletrendszerek megoldása Newton-módszerrel	335
A Jacobi-mátrix közelítéséről	338
A Broyden-módszer	340
A folytatás módszere	341
Szélsőérték feladatok	344
Gradiens módszerek	345
Newton-eljárások	351
A Gauss-Newton módszer	355
További nemlineáris feladatok és megoldási módszerek	362
Összefoglalás	363
Feladatok	363
Jelölések	370
Irodalomjegyzék	372
Tárgymutató	377
Címszavak jegyzéke	377
Tételek, lemmák jegyzéke	386
Algoritmusok jegyzéke	388

Témakörök

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem