1.119.677
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Számolóábrák egyszerű készítése
| Kiadó: | Műszaki Könyvkiadó |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Fűzött keménykötés |
| Oldalszám: | 207 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Fekete-fehér ábrákkal illusztrálva. Tankönyvi szám: 48/68. Készült 1000 példányban. 4 kivehető melléklettel. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
E könyv megírásakor azt a célt tűztem magam elé, hogy megismertessem az olvasót - csupán középiskolai matematikai ismeretek alapján - a számolóábrák (nomogrammok) készítésével. Ezt azért tartottam... TovábbElőszó
E könyv megírásakor azt a célt tűztem magam elé, hogy megismertessem az olvasót - csupán középiskolai matematikai ismeretek alapján - a számolóábrák (nomogrammok) készítésével. Ezt azért tartottam szükségesnek, mert tapasztalatom szerint technikusaink és mérnökeink nem elég járatosak a „klasszikus" nomográfia megértéséhez szükséges determináns elméletben. Éppen ezért nem indulhattam ki a szokásos Soreau-féle osztályozásból és nem használhattam fel Cauchy és Clark kanonikus alakjait. Ennek ellenére úgy érzem,[könyvem rendszere a gyakorlat szempontjából kielégítő. Feladatomnak tartottam, hogy lehetőleg átfogó munkát adjak az olvasó kezébe, annál is inkább, mert ilyen a világirodalomban is csak nagyon kevés található. Az egyik szerző csak a pontsoros, a másik csak a görbesereges nomogrammok ismertetésére szorítkozik, legtöbbször ezek közül is csak egyes típusokat ismertet és így, ha a gyakorlatban egy képlethez valaki nomogrammot kíván készíteni, nem kap kellő áttekintést a lehetőségekről és a célnak legjobban megfelelő ábratípusról. Rendkívül érdekelne az olvasók véleménye, hogy célkitűzésemet mennyire sikerült elérnem és hogy könyvemről akár érthetőség, akár teljesség szempontjából hogyan vélekednek. Köszönetet mondok végül e helyen Orilódy János, Pálmai) Lóránd és Pöhm György kartársaimnak, kik tanácsaikkal e könyv megírásában segítettek. VisszaTartalom
| Bevezetés | 5 |
| A függvényekről általában | 5 |
| Grafikus számolás | 6 |
| A számolóábrák fajtái | 8 |
| A beosztások | 8 |
| Áttérés egyik osztásrendszerről a másikra | 12 |
| Számolóábrákkal elérhető pontosság és a pontosság növelésének lehetőségei | 13 |
| Osztáspapirok | 13 |
| Kétváltozós függvények számolóábrái | 14 |
| Kétváltozós függvények hálósábrái | 14 |
| Kétváltozós függvények pontsoros ábrái | 21 |
| Háromváltozós, minden változót csak egy alakban tartalmazó függvények számolóábrái | 22 |
| E függvények ábrázolása hálósábrákkal | 22 |
| Alapműveletek | 22 |
| Bonyolultabb függvényalakok | 26 |
| Háromszögábrák | 26 |
| Háromváltozós, minden változót csak egy alakban tartalmazó függvények pontsoros ábrái | 34 |
| Összeadás-kivonás | 34 |
| Szorzás-osztás | 37 |
| Hatványozás-gyökvonás | 40 |
| A dualitás elve és alkalmazása | 41 |
| Háromváltozós, az egyik változót két alakban tartalmazó függvények számolóábrái | 47 |
| Görbesereges ábrák készítése a fenti függvényekhez | 48 |
| Egyenesekkel ábrázolható, egy változót két alakban tartalmazó, háromváltozós függvények nomogrammjai | 48 |
| Háromváltozós, egy változót két alakban tartalmazó függvények pontsoros ábrái | 54 |
| Szerkesztés a dualitás elve alapján | 51 |
| A görbe pontsor pontjainak közvetlen szerkesztése a hálós ábra nélkül | 51 |
| A görbe pontsor pontjainak kiszámítása. (A görbe egyenlete) | 55 |
| Általánosított eset: a pontsoros ábra két egymást metsző egyenesből és egy görbéből áll | 57 |
| Háromváltozós, két változót két alakban tartalmazó függvények nomogrammjai | 62 |
| Görbesereges ábrák készítése a fenti függvényekhez | 62 |
| Egyenesekkel ábrázolható, háromváltozós, két változót két alakban tartalmazó függvények hálós ábrái | 64 |
| Háromváltozós, két változót két alakban tartalmazó függvények pontsoros ábrái | 71 |
| Szerkesztés a dualitás elve alapján | 71 |
| A görbe pontsorok pontjainak közvetlen megszerkesztése | 71 |
| A görbe pontsorok egyenlete | 72 |
| Pontmezős nomogrammok készítése | 74 |
| Négyváltozós, minden változót egy alakban tartalmazó függvények nomogrammjai | 78 |
| Négyváltozós, minden változót egy alakban tartalmazó függvények hálós ábrái | 88 |
| Négyváltozós, minden változót egy alakban tartalmazó függvények pontsoros nomogrammjai | 88 |
| Négyváltozós, pontsoros összeadó nomogrammok | 88 |
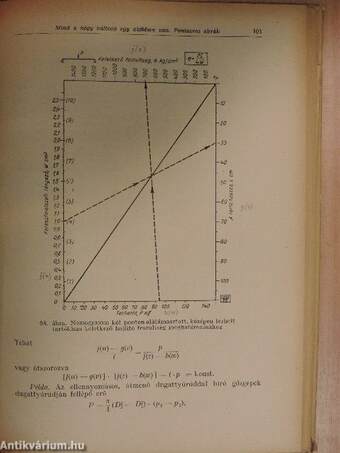
| Négyváltozós, a változókat összeadáson (kivonáson) kívül szorzási (osztási) műveletekkel összekötő függvények pontsoros számolóábrái | 91 |
| Négyváltozós, egy vagy két változót két alakban tartalmazó függvények | 104 |
| Hálós ábrák készítése a fenti függvényekhez | 104 |
| Négyváltozós, egy vagy két változót két alakban tartalmazó függvények pontsoros nomogrammjai | 106 |
| Négynél több változót tartalmazó függvények kombinálatlan nomogrammjai | 115 |
| Hálós ábrák kombinációja hálós ábrákkal | 115 |
| Négynél több változót tartalmazó függvények pontsoros ábrái | 122 |
| Ábrakombinációk | 135 |
| Hálós ábrák kombinációja hálós ábrákkal | 135 |
| Görbesereges és pontsoros ábrák kombinációja | 140 |
| Pontsoros nomogrammok kombinációja | 144 |
| Transzformáció | 146 |
| Görbesereges nomogrammok transzformációja | 146 |
| Pontsoros nomogrammok transzformációja | 150 |
| Mozgóalkatrészes nomogrammok | 166 |
| Mozgóskálás nomogrammok | 166 |
| Mozgólapos nomogrammok | 171 |
| Összefoglalás és áttekintés | 178 |
| Nomogrammok szerkesztésének menete | 178 |
| Az ismertetett nomogrammtípusok összefoglalása | 182 |
Témakörök
Sors László
Sors László műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Sors László könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.