A geostatisztika alapjai

Szerző

Steiner Ferenc

Lektor

Dr. Csernyák László

Budapest

'Steiner Ferenc: A geostatisztika alapjai ' összes példány

Kiadó:	Tankönyvkiadó Vállalat
Kiadás helye:	Budapest
Kiadás éve:	1990
Kötés típusa:	Fűzött kemény papírkötés
Oldalszám:	363 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	24 cm x 17 cm
ISBN:	963-18-2819-0
Megjegyzés:	A könyv fekete-fehér ábrákkal illusztrált. Kihajtható mellékletekkel. Tankönyvi száma: 44546. 1000 példányban jelent meg.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Fülszöveg

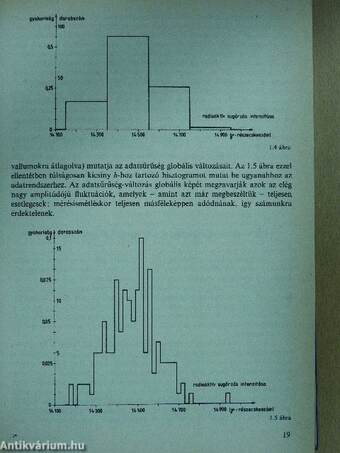
Lezárul egy felhőtlenül boldog korszak a statisztika gyakorlatában: a szakemberek többsége ui. eddig kételyek nélkül hitt abban, hogy a hibaeloszlások gyakorlatilag mindig Gauss-típusúak (vagy legalábbis Gauss-határeloszlásúak), s így lelkiismereti aggály nélkül alkalmazták az erre alapozott módszereket, amelyeket egy szinte esztétikailag is tökéletes elmélet fogott keretbe.
A valóságban előforduló sokféle hibaeloszlást statisztikailag optimálisan kezelni tudó elmélet gyakorlati alkalmazásának azonban már immár nincsenek számításgazdaságossági akadályai, így a Gauss-eloszlás túlnyomó előfordulásának dogmáját tovább már semmilyen szempontból sem lehet elfogadni. Az eddigieknél sokkal általánosabb szemléletű bevezető összefoglalásra tehát a praxisnak sürgetően szüksége van, különösen olyan szakterületeken, mint pl. a geostatisztika, ahol megengedhetetlen az adatok jelentős százalékának figyelmen kívül hagyása, márpedig a hagyományos eljárások kis statisztikai hatásfoka gyakorlatilag valóban egyet jelent azzal, hogy drágán beszerzett adataink egy részét eltékozoljuk.
A valószínűségi törvényszerűségek és a statisztikai "beavatkozás" modern információelméleti szemléletmódja szilárd elvi alapot ad témánk kellően általános tárgyalására, ugyanakkor - heurisztikus gondolatmenetek bőséges közlésével - célszerű az induktív és deduktív szemlélet kellő egyensúlyára törekedni, hogy a lényeget ne csak tudni, hanem "érezni" is lehessen. Ez a záloga ui. annak, hogy az olvasó a könyv által ismertetett alapokból kiindulva ne csak gépies alkalmazásra legyen képes, hanem alkotó applikálásra, ill. továbbfejlesztésre is. A bemutatott példák elemi, speciális szakismeretet nem feltételező volta a könyv anyagának elsajátítását - az olvasó szakterületétől függetlenül - mindenki számára lehetővé teszi, aki a statisztika alkalmazója kíván lenni, és ehhez modern bevezető összefoglalást igényel. Vissza

Tartalom

Előszó	11
Adatrendszerek, hisztogramok és sűrűségmodellek	15
Adatrendszerek ábrázolása. Hisztogram	16
Adatrendszer ábrázolása a számegyenesen	16
Adatok előfordulási számának ábrázolása	17
A hisztogram	17
Adatsűrűség-modellek, sűrűségfüggvények	20
Nevezetes adatsűrűság-modellek	21
Az egyenletes adateloszlás sűrűségfüggvénye	21
A Gauss-féle sűrűségfüggvény	21
A Laplace-féle sűrűségfüggvény	22
A Cauchy-féle sűrűségfüggvény	22
A helyparaméter és a skálaparaméter fogalma	23
A sűrűségmodell illesztése az adatrendszerekre	25
A legkisebb négyzetek elve	25
Az illesztés gyakorlati végrehajtása	27
Modellcsaládok (ún. szupermodellek)	30
Szimmetrikus szupermodellek	30
Az fa(X) szupermodell	30
Az fp(X) szupermodell	33
Az f alfa (X) szupermodell	34
Asszimetrijus szupermodellek	35
A Weibull-féle szupermodell	38
A lognorm-szupermodell	38
A gamma-szupermodell	39
A béta-típuscsalád	41
Az F-szupermodell	42
Az aszimmetrikus szupermodellek "negatív" variánsai	44
Kumulatív gyakorisági hisztogramok és jellemzésük a sűrűségfüggvények integráljaival	45
A kumulatív gyakoriságok hisztogramjai	46
Eloszlásfüggvények	48
Az eloszlásfüggvény definíciója, kapcsolata a kumulatív gyakorisági hisztogrammal	48
Néhány analitikusan adott eloszlásfüggvény	49
Néhány szó az eloszlásfüggvények inverz függvényéről	52
Kiegészítés a sűrűségfüggvényekhez, ill. szupermodellekhez	54
A logisztikus modell	54
Slash-modell	54
Az f fia (x) szupermodell	55
Az exponenciális modell	55
A Pareto-féle szupermodell	55
A kettős exponenciális modell és az FII (X) szupermodell	56
A legjellemzőbb érték meghatározása	59
Minta alapján meghatározott jellemző értékek	60
A mintamedián (med n)	60
A számtani átlag (E n)	61
A leggyakoribb érték (M n)	64
Iteráció rögzített szélességű súlyfüggvénnyel	64
A súlyfüggvény szélességparaméterének a meghatározása. Maximális effektív adatszám követelése az M körül minél rövidebb intervallumon	66
M n és E együttes meghatározása	69
Az általánosított leggyakoribb érték (M k;n)	71
Egyéb mintajellemzők	72
Az alfa-levágott átlag	72
Az alfa-winsorizált átlag	72
A Hodges-Lehmann-becslés	72
Sűrűségfüggvények alapján meghatározott jellemző értékek	73
Általános formulák	73
Leggyakoribb értékek, mediánok és várható értékek különböző aszimmetrikus modellekre	77
Az adatrendszerben rejlő bizonytalanság jellemzése. Az egyes adatok hibái	80
Adatrendszer "távolsága" egyetlen adat x 0 értéktől	81
Meggondolások egyetlen adat x 0-tól való távolságára	81
Adatrendszer távolsága x 0-tól	82
Az adatrendszer legjellemzőbb értéke mint valamely norma minimumhelye	84
Az adatrendszerben rejlő bizonytalanság mint a norma értéke a minimumhelyen. Hibaformulák	88
A dihézió mint hibajellemző	93
Dihéziótáblázatok, szórásformulák	94
Az adatrendszerben rejlő bizonytalanság jellemzése különböző konfidenciaszintekhez tartozó intervallumokkal	100
Konfidenciaintervallumok; ezek félterjedelmei mint hibajellemzők	101
Az egyes hibajellemzők közötti kapcsolat	104
Valószínűségelméleti összefoglalás	110
A valószínűség és a valószínűségi változó fogalma	110
Bevezető meggondolások	110
A valószínűség fogalmának heukrisztikus bevezetése	112
A Kolmogorov-féle fogalom- és axiómarendszer	114
Valószínűségi változók	116
Többváltozós sűrűség- és eloszlásfüggvények. A feltételes valószínűség fogalma	119
Többváltozós sűrűség- és eloszlásfüggvények és egymással való kapcsolatuk	119
A feltételes valószínűség fogalma	122
Valószínűségi változó várható értékeire vonatkozó tételek	125
Megjegyzések a várható érték és szórásnégyzet fogalmához és jelöléséhez	125
Fontosabb tételek a várható értékekre	127
A kovariancia fogalma	128
Definíció és diszkusszió	128
A korrelációs együttható hagyományos definíciója	129
Valószínűségi változók összegének szórásnégyzete	130
Az összegformula levezetése	130
Tetszőleges lineáris kombináció szórásnégyzete	131
Néhány tétel valószínűségi változók szórásnégyzeteire	131
Tételek	131
Közvetetten meghatározott mennyiség hibájának a kiszámítása	133
Matematikai statisztika	135
A matematikai statisztika szemlélete és kérdésfeltevései	135
A statisztikai minta	135
Néhány alapkérdés	136
Mintavétel tetszőleges valószínűségeloszlásból Monta Carlo-módszerrel	138
Az "ideális minta" fogalma	139
Maximum likelihood-típusú becslések (ún. M-becslések)	141
Valószínűségeloszlások paramétereinek maximum likelihood-becslése	141
M-becslések	145
Az I-divergencia minimalizálása	148
Helyettesítő eloszlások	148
Az információveszteség minimalizálása	148
Általános formulák	149
Az információveszteség minimalizálása Gauss-eloszlással történő helyettesítéskor	150
Az információveszteség minimalizálása Cauchy-eloszlással történő helyettesítéskor	151
Megjegyzések	152
Az IC-függvény	153
Az IC-függvény definíciója	153
Az IC-függvény számítása fi-és X-függvényekből	154
A leggyakoribb érték számításának IC-függvénye	156
Becslések határeloszlásai. A nagy számok törvényének teljesülési üteme	158
Összeg és átlag sűrűségfüggvénye	158
A karakterisztikus függvény fogalma	165
Számtani átlagok határeloszlása véges o esetén. A centrális határeloszlástétel	170
Megjegyzések a nagy számok törvényének teljesüléséhez, ill. teljesülési üteméhez	175
Becslések aszimptotikus szórása	180
Az aszimptotikus szórásnégyzet általános formulája	180
A leggyakoribb értékek aszimptotikus szórásai	184
A statisztikai hatásfok	187
A Cramér-Rao-határ	187
Az abszolút és relatív hatásfok definíciója	189
Az általános leggyakoribb értékek és fokozott rezisztenciájú változatainak abszolút hatásfokai	194
A hibameghatározás bizonytalanságai	200
Az empirikus szórás meghatározási hibája	200
A valószínű hiba empirikus értékének meghatározási bizonytalansága	202
A dihézió meghatározásának bizonytalansága	203
Statisztikai próbák	205
Statisztikai próbák az adatok ismert eloszlástípusa esetén	205
Bevezető meggondolások. Egyszerű próba a T helyparaméterre	205
Statisztikák és sűrűségfüggvényeik az adatok ismert eloszlástípusára	209
Eloszlástípusra vonatkozó próbák és meggondolások	214
A Kolmogorov-próba	214
Típusra vonatkozó grafikus próbák	217
C-próba az fa(X) szupermodellre	226
A típusmeghatározás további lehetőségeiről	232
A korreláció fogalma. A lineáris függés mérőszámának meghatározása	235
Bevezetés és problémafelvetés	235
Az alfa(x) eloszlások stabilitása és hasonlóságuk az alfa (x) eloszlásokhoz	241
A stabilitás fogalma	241
Az alfa (x) eloszlások stabilitása	242
Az alfa (x) és az f a (x) eloszlások hasonlósága	243
Adott mértékű lineáris függés generálása két valószínűségi változó között	248
A lineáris függés mérőszámának meghatározása	249
A függés érzékelése különbségi- és összeg-adatrendszerekkel	249
Az /r/ meghatározása az S-, S+ síkon	250
Közelítő formulák	254
A korrelációs együttható hagyományos meghatározása, ill. definíciója. A kovariancia fogalma	257
Megjegyzések a kétváltozós Gauss-eloszláshoz	261
Általános megjegyzések	261
Az r-értékek hibája	265
Függetlenségvizsgálat	266
Többváltozós összefüggések korrelációs jellemzése	267
A korrelációs mátrix (R) és a kovarianciamátrix (C)	267
A kiegyenlítéssel kapott együtthatók B mátrixának összefüggése C-vel és R-rel	269
A parciális korrelációs együtthatók	271
A többszörös korrelációs együttható és a determinációs együttható fogalma	272
Néhány szó a nemlineáris függés esetéről, valamint függésről korrelálatlanság esetén	273
Korrelációs kapcsolat jellemzése nemlineáris esetben. A korrelációs index fogalma.	273
A korreláció mértéke	273
Függés korrelálatlanság esetén	275
Következtetés be nem mért térrészek jellemzőire. Krigelés és interpolálás	277
A krigelés	277
A variogram	278
Kovariancia meghatározása a variogram alapján	280
A kovariancia és variogram irányfüggése	281
A variogram és az autokorrelációs függvény kapcsolata	281
Variogram-modellek	284
Következtetés be nem mért térrészek jellemzőire krigeléssel	285
A becslés varianciájának minimalizálása	285
A blokk-krigelés	287
Egyéb krigelési eljárások	288
Példa a krigelés gyakorlati végrehajtására	289
Megjegyzések a krigeléshez	293
Interpoláció	299
A krigelés mint interpolációs eljárás	299
Egyéb interpolációs eljárások	300
A szinusz kardinálisz függvénnyel történő interpoláció	301
Spline-interpoláció	303
Lokálisan független interpolációs eljárások	304
Megjegyzés az interpolációs eljárásokhoz	306
Kiegyenlítések. Többváltozós (lineáris és nemlineáris) regresszió	308
Interpoláció és kiegyenlítás (bevezetés)	308
Általános kiegyenlítési alapelvek	309
A legkisebb négyzetes, valamint a leggyakoribb érték szerinti kiegyenlítés gyakorlati végrehajtása	312
A kiegyenlítések végrehajtásához szükséges adatmennyiségről	316
A leggyakoribb érték szerinti kiegyenlítés, és a hibaeloszlás entrópiája	319
Gyakorlati példák az M- és az E-kiegyenlítés összehasonlítására	321
Egyenes-kiegyenlítések	321
A mágneses normáltér példája	322
Hatváltozós kvadratikus kiegyenlítés a permeabilitásnak egyéb adatokból való meghatározása	324
Példa az M- és E-kiegyenlítés súlyozott változataira	325
A q(H) függvénykapcsolat meghatározása dihéziók számításával	325
Gravitációs példa a súlyszámítás bemutatására, valamint a súlyozott kiegyenlítések	329
Spline-kiegyenlítés. (Példa a pontosan teljesítendő feltételekre a paraméterek között)	331
Szupermodellek, normák, adatrendszer-jellemzők, bizonytalansági jellemzők, valamint a kiegyenlítési eljárások kölcsönös kapcsolata	333
Köszönetnyilvánítás	334
Függelék	335
Integrálok gyors számítása	335
Függelék	338
Fourier-transzformációk	338
Definíciók és tételek	338
A Dirac-delta-függvény	340
Függelék	343
Diszkrét eloszlások. A X2-próba	343
Függelék	349
Táblázatok	349
Számtáblázatok jegyzéke	353
Formulatáblázatok	354
Irodalomjegyzék	355
Név- és tárgymutató	359

Témakörök

Steiner Ferenc

Steiner Ferenc műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Steiner Ferenc könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem