1.127.060
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Szimmetria és struktúraépítés
Eötvös Loránd Tudományegyetem Természettudományi Kar/Kézirat
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 260 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | A kézirat 228 példányban jelent meg 108 fekete-fehér ábrával, kihajtható mellékletekkel. Tankönyvi szám: J 3-1441. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
A speciálkollégium az a terület, ahol az egyetemi oktatók új oktatási és kutatási módszereket mutathatnak be a hallgatóknak. Formába önthetnek új ismeretrendszereket, s ezek mint a szellemi alkotás... TovábbElőszó
A speciálkollégium az a terület, ahol az egyetemi oktatók új oktatási és kutatási módszereket mutathatnak be a hallgatóknak. Formába önthetnek új ismeretrendszereket, s ezek mint a szellemi alkotás nagymolekulái kerülnek megmérettetésre. E megmérettetés a használhatóságon, összerendező képességen, továbbfejleszthetőségen és számos egyéni jellemzőn (áttekinthetőség, vizuális kíséret) át történik.Ez a munka a technika szak tantárgyrendszerébe illeszkedik. Felépítésében három rendező elvre alapoz: a szimmetriára, a hierarchiára és a dimenzionalitásra. De gondolat és tevékenységébresztő vezérfonál e munka a kidolgozás formájában is: olyan új műveleteket vezet be, melyek jól áttekinthető készletekhez vezetnek egy-egy vizsgálatra kiszemelet feladatkörben. E készletek - mátrixok, táblázatok - magot képeznek. Magot, melyhez eljutni az ismétlődő elemektől a kiválasztott művelettel egyszerű. Magot, melyhez alkalmazásokat, továbbfejlesztéseket kapcsolni kívánatos és élményt adó. Magot, melyet elraktározni az emlékezetbe vizualitásánál és egyszerűségénél fogva könnyű. A kedv és a tevékeny lelkesedés fölébresztése és fönntartása e tanulányok során éppúgy elérendő cél, mint új ismeretcsokor kötése és szerteágazásainak bemutatása. E szerteágazások egybefonódása új rendező elveken építkezve, szeretném, ha követésre biztató lenne új ismeretmolekula-konstruáló tanárkollégák számára. Vissza
Tartalom
| Elemeket szervező dualitások | 9 |
| Bevezető gondolatok | 9 |
| Tárgyunk kapcsolata az Anyagtechnológiával | 10 |
| Fölépítés-lebontás | 12 |
| Egybevágó elemek készletei az Univerzumban | 16 |
| Globális-lokális | 18 |
| Jelenségkeretek merev struktúrákhoz kristály és bolygótest (elektromágnesség-gravitáció) | 18 |
| Rendezettség-rendezetlenség | 21 |
| Három közös rendezőelv: szimmetria, hierarchia, dimenzionalitás | 24 |
| Rend és készlet | 31 |
| Alakzatrendszerek | |
| A szimmetria a technika, a művészet és a tudomány közös fogalma | 31 |
| A szimmetria és a transzformációk | 32 |
| A szimmetria és az információk | 35 |
| A szimmetrikus alakzat szerveződésének kiolvasása | 36 |
| A szerveződések alapkészletei a síkon | 37 |
| A szimmetria és a techné | 44 |
| Frízek és szálak - szövés | 55 |
| Alakzatrendszerek hierarchiával | |
| A hantik (osztyákok) kétszínű frizmozaikjai | 56 |
| Frízek kettőzése | 61 |
| Fríz-kettősfríz-tapétacsoport szerveződésrendszer a honfoglaláskori régészeti leleteken | 62 |
| Avar-onogur kettősfrízek | 69 |
| Alapfrízekből szőtt tapétacsoport-mintázatok | 71 |
| A kettősfrízek technológiai eredete | 73 |
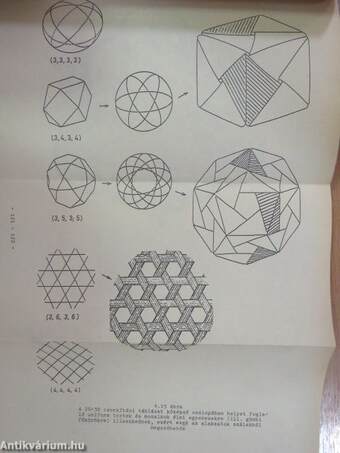
| Szakaszok, lapok, testek - átépítés csonkítással | 79 |
| Szabályos sokszögkarám építése a síkon | 85 |
| Szabályos és félig szabályos testek és mozaikok | 86 |
| A szabályos testek száma az euklideszi térben | 88 |
| A csonkítással rendszerező táblázat | 91 |
| A 3D tér kockarácsa | 104 |
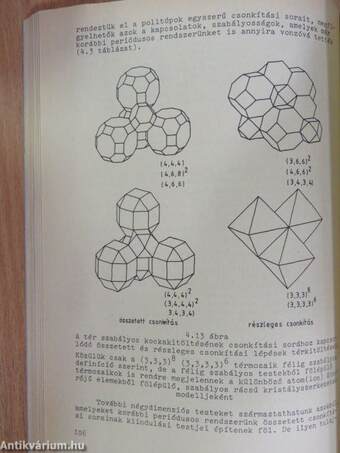
| A 4D testek és 3D mozaikok csonkítási táblázata | 105 |
| A 4D két szabályos térrács-sorozata és az 5D testek csonkítási táblázata | 112 |
| A csonkítási táblázat kapcsolatai technológiákkal | 119 |
| Pedersen megszőtt szabályos és félig szabályos testjei | 119 |
| Gyűrűkapcsolások Escher egy grafikáján | 119 |
| Gömhéjépítészet | 125 |
| Rétegek a kristályokban | 129 |
| A valódi kristályok szerkezete | |
| Rétegek a kristályszerkezetben | 129 |
| Kristályok külső és belső rendje | 130 |
| Globális és lokális rácstulajdonságok | 134 |
| Barlow tétele | 137 |
| Kvázikristályok | 139 |
| Rétegek és valódi kristályok szerkezetében (Dódony István) | 144 |
| Rendezettség a szilárd anyagszerveződések különböző hierarchiaszintjein | 150 |
| Léptékváltó alakzatrendszerek: növények és fraktálok | 150 |
| A növények felszíni rácsrendje | 159 |
| Fibonacci-növények | 164 |
| Transzformációk | 166 |
| Analitikus eset | 167 |
| A Fibonacci-növények modellrendszere | 168 |
| A sejtautomata modell | 177 |
| A hengerszimmetrikus rácsok általános tulajdonságai | 180 |
| Deformáció-ekvivalens rácsok osztályai a hengeren | 182 |
| Fraktálok természeti és művészeti példákkal | 189 |
| Az ornamentikától a negyedik dimenzióig | 199 |
| Alakzatrendszerek intuitív művészeti-technikai fejlesztése | |
| Közösségi művészet | 199 |
| A díszítőművészet kommunikációs nyelv | 199 |
| Állandóság | 206 |
| Változtatások | 211 |
| Egyediség-egyéniség | 212 |
| Fejlesztések műveltségi közösségekben | 213 |
| Avar-onogurok | 213 |
| Altáji szkíták rátétes struktúrái | 214 |
| Az m-g kettősfriz forráshelye | 217 |
| Egyéni alkotók - M. c. Escher, S. Dali és egy hazai kortárs | 226 |
| Függelék | 239 |
| Irodalom | 251 |
| Tartalom | 257 |
Bérczi Szaniszló
Bérczi Szaniszló műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Bérczi Szaniszló könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.