Válogatott tanulmányok

Szerző

Gábor Dénes

Szerkesztő

Fordító

Lektor

Budapest

'Gábor Dénes: Válogatott tanulmányok ' összes példány

Kiadó:	Gondolat Könyvkiadó
Kiadás helye:	Budapest
Kiadás éve:	1976
Kötés típusa:	Fűzött keménykötés
Oldalszám:	416 oldal
Sorozatcím:	Válogatott tanulmányok
Kötetszám:
Nyelv:	Magyar
Méret:	19 cm x 13 cm
ISBN:	963-280-196-2
Megjegyzés:	Fekete-fehér fotókkal és ábrákkal illusztrálva.

Értesítőt kérek a kiadóról

Értesítőt kérek a sorozatról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

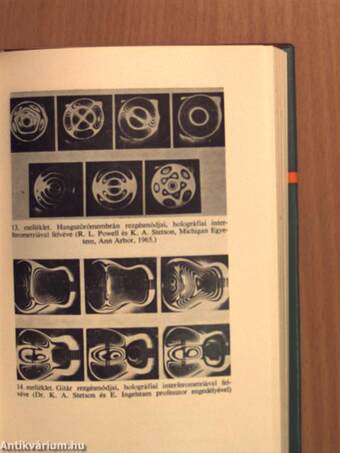
HOLOGRÁFIA
Holográfia, 1948-1971	11
Új mikroszkópelv	48
Holográfia, avagy az "egész kép"	53
Optikai képszintézis (komplex amplitúdóösszegezés és -kivonás) holografikus Fourier-transzformációval	68
A mély hologramok elmélete	72
Bevezetés	73
A mély hologramok rögzítésének és rekonstrukciójának általános formulái	77
A felvétel	80
A rekonstrukció	81
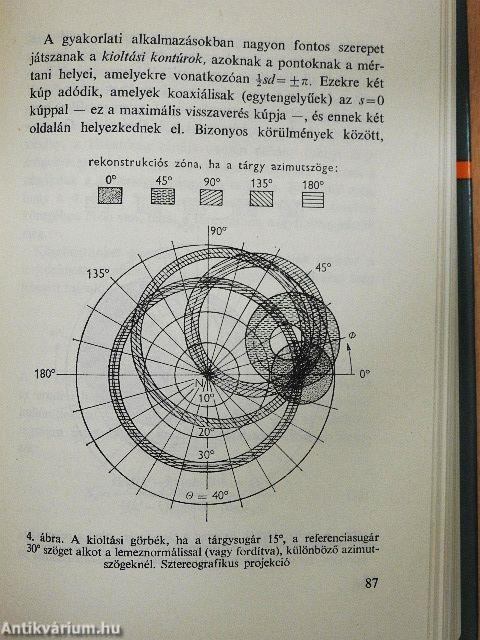
Irányszelektivitás	83
Színszelektivitás	89
A másodikhullám	91
Rendezetlen hologramban milyen formában tárolódik az információ?	92
A jelenergia	93
Rendezetlen hologram autokorrelogramja	95
Holografikus memóriák	103
Az időbeli visszaállítás holográfiai modellje	103
Az időbeli visszaállítás tökéletesített holográfiai modellje	105
Asszociatív holografikus memóriák	108
Betűfelismeres holográfiával	122
INFORMÁCIÓELMÉLET
A hírközléselmélet és a fizika	133
A jelek klasszikus leírása	135
Az információcella statisztikai tulajdonságai	138
A jelek statisztikája	145
Kapcsolat a kvantumelméleti és a klasszikus leírás között	149
Információcela energiaingadozásai jel jelenlétében (1. függelék)	164
Klasszikus energia kicserélődés hullám és elektronnyaláb között (2. függelék)	166
Energiakicserélődés elektronok és gyenge erőterek között a kvantummechanika szerint (3. függelék)	171
Elektromos erőterek elektronokkal való optimális letapogatásának a feltételei (4. függelék)	182
Információelmélet és kibernetika	186
Strukturális információelmélet	187
Statisztikai információelmélet	195
Szűrés, előrejelzés és felismerés	203
A sorfejtési tétel (1. függelék)	219
Hulllámalakok és információs szimbólumok (2. függelék)	225
Nonlineáris optimális szűrők (3. függelék)	232
Akusztikai kvantumok és a hallás elmélete	236
ELEKTRONFIZIKA
Elektronnyalábok dinamikája. A Hamilton-egyenletek alkalmazása elektronproblémák megoldására
A problémakör áttekintése	253
Egyetlen elektron mozgása. A Hamilton-féle kanonikus egyenletek	255
A Lagrange-invariáns	258
A Lagrange-tétl alkalmazása elektronnyalábokra	262
A Hamilton-Jacobi egyenlet	266
A Hamilton-Jacobi-egyenlet alkalmazása	269
Az elektronok mozgása gyorsan változó terekben (Futásidő-hatások)	282
Rendezetlen mozgást végző elektronnyalábok	291
Az elektroneloszlás stacionárius elektromágneses terekben	293
Elektroneloszlás gyorsan változó terekben	297
Konklúzió	297
Hamilton kanonikus egyenleteinek bizonyítása (1. függelék)	298
A Lagrange-tétel bizonyítása (2. függelék)	300
Reguláris elekronnyalábok totális impulzusának rotációja (3. függelék)	301
Louis de Broglie és a látható világ határai	304
A Langmuir-paradoxon	319
A plazma hullámelmélete	330
Bevezetés	331
A plazmahullámok spektrális energiaeloszlási törvénye	334
A plazmahullámok energiájának termodinamikai felső határa	340
Az elektronok szóródása plazmahullámokon	344
Az elektrondiffúzió	345
Az elektronok energiakicserélődése	354
Konklúzió	356
A TUDOMÁNY FELELŐSSÉGE
A tudomány új felelősségei	361
Számos kritikus pont	365
Az infláció más megközelítése	369
Számítógépes előrejelzés	373
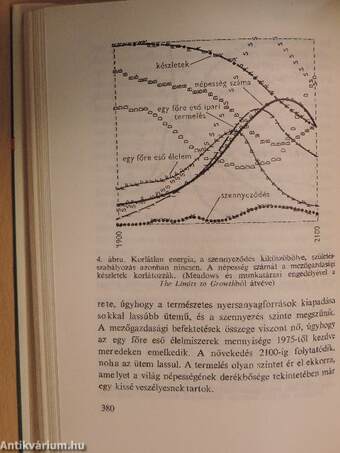
A természetes nyersanyagforrások kimerülése	381
Gábor Dénes közleményei	390
Utószó	404