1.120.306
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát
Valószínüségszámítás
A matematikai statisztika elemei/Kézirat
| Kiadó: | Tankönyvkiadó Vállalat |
|---|---|
| Kiadás helye: | Budapest |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 259 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Magyar |
| Méret: | 24 cm x 17 cm |
| ISBN: | |
| Megjegyzés: | Kézirat. Fekete-fehér ábrákkal illusztrálva. Tankönyvi szám: J9-868. Megjelent 345 példányban. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
A müszaki tudományok fejlődése jelenlegi szakaszának egyik jellemzője, hogy egyre szélesebb körben és nagy haszonnal alkalmazza a valószínüségszámitás és a matematikai statisztika módszereit a... TovábbElőszó
A müszaki tudományok fejlődése jelenlegi szakaszának egyik jellemzője, hogy egyre szélesebb körben és nagy haszonnal alkalmazza a valószínüségszámitás és a matematikai statisztika módszereit a törvényszerüségek feltárása, a jelenségek lefolyásának előrelátása céljából. Ezt a tendenciát természetesnek kell tartanunk, a jelenségek valamely körének elmélyült tanulmányozása során elkerülhetetlenül bekövetkezik ez a szakasz. Amikor valamely fizikai, technikai folyamatot, jelenséget vizsgálunk, nyilván arra törekszünk, hogy meghatározzuk azokat a fő feltételeket, komponenseket, amelyek a jelenség lefolyását döntőleg meghatározzák. Ezután megvizsgáljuk, hogy ezek az alapvető feltételek, döntő körülmények hogyan hatnak a jelenség lefolyására, s a felismert törvényszerüséget igyekszünk matematikailag kifejezni valamilyen függvénykapcsolat formájában. VisszaTartalom
| Alapfogalmak | 9 |
| A véletlen esemény matematikai fogalma | 9 |
| A valószinüség fogalma | 13 |
| Valószinüségszámitási axiómák és tételek | 16 |
| Valószinüségek közötti összefüggések | 18 |
| A valószinüségek klasszikus kombinatorikus kiszámitási módja | 22 |
| Feltételes valószinüség és függetlenség | 28 |
| Valószinüségi változók és valószinüségeloszlások | 34 |
| A valószinüségi változó és a valószinüségeloszlás fogalma | 34 |
| Diszkrét valószinüségi változók | 39 |
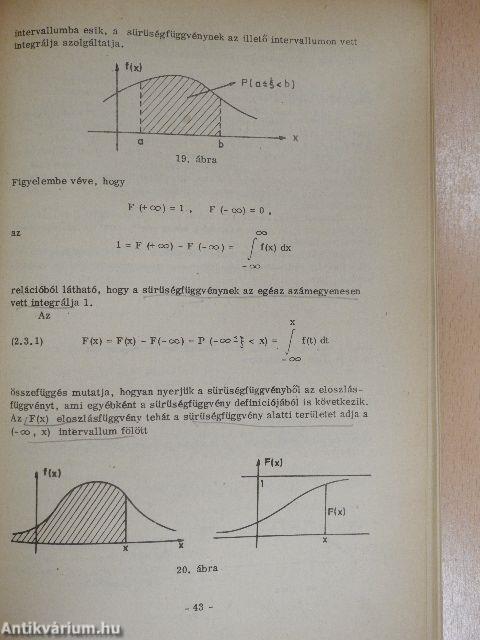
| Folytonos valószinüségi változók | 41 |
| A többdimenziós valószinüségeloszlás fogalma és valószinüségi változók függetlensége | 45 |
| Valószinüségi változók függvényeinek eloszlása | 56 |
| Valószinüségi változó monoton függvényének eloszlása | 56 |
| Független valószinüségi változók összegének, szorzatának és hányadosának eloszlása. Kompozició | 57 |
| A valószinüségeloszlások jellemző adatai | 61 |
| A várható érték fogalma és tulajdonságai | 61 |
| A feltételes várható érték | 68 |
| A szórás fogalma és tulajdonságai. Csebisev-tétele | 70 |
| A valószinüségi változó momentumai | 74 |
| A korrelációs együttható | 77 |
| A generátorfüggvény és a karakterisztikus függvény | 81 |
| A generátorfüggvény | 81 |
| A karakterisztikus függvény | 83 |
| Fontosabb valószinüségeloszlások | 87 |
| Diszkrét valószinüségeloszlások | 87 |
| Egyszerü alternativa | 87 |
| Binomiális vagy Bernoulli-eloszlás | 87 |
| A binomiális eloszlás közelitése. Moivre-Laplace határeloszlás tétel | 92 |
| Poisson-eloszlás | 93 |
| A polinomiális-eloszlás | 96 |
| A geometriai-eloszlás | 97 |
| Folytonos eloszlások | 98 |
| A normális eloszlás | 98 |
| A többdimenziós normális eloszlás | 107 |
| A logaritmikus normális eloszlás | 110 |
| Az egyenletes eloszlás | 112 |
| A gamma-eloszláscsalád | 114 |
| A nagy számok törvényének Bernoulli-féle alakja | 118 |
| A központi határelosztás tétel | 121 |
| Markov-láncok | 125 |
| A Markov-lánc fogalma | 12 |
| A Markov-láncok alkalmazása viztározókkal kapcsolatban | 136 |
| A matematikai statisztika tárgya. A statisztikai minta és jellemzői | 141 |
| A minta fogalma | 145 |
| A statisztikai minta jellemzői | 147 |
| A minta jellemzőinek várható értéke és szórása | 151 |
| Becsléselmélet | 155 |
| A becslés fogalma és tulajdonságai | 155 |
| A becslés módszere. Maximum-likelihood-módszer | 163 |
| A becslés megbizhatósága | 168 |
| Statisztikai hipotézisek vizsgálata | 172 |
| Elvi megjegyzések | 172 |
| Az u-próba. Első és másodfaju hiba | 178 |
| Az erőfüggvény | 182 |
| A Student-féle t-próba | 184 |
| Szekvenciális módszer hipotézisvizsgálatra | 186 |
| Nemparaméteres-próbák | 195 |
| A rendezett minták elméletének elemei | 196 |
| Kolmogorov-Szmirnov tipusu határeloszlások és statisztikai alkalmazásuk | 199 |
| További módszerek illeszkedésvizsgálatra | 207 |
| Normalitás-vizsgálat | 207 |
| A x2-próba | 210 |
| A minta véletlenségének vizsgálata | 217 |
| Hibaelmélet | 220 |
| Közvetlen megfigyelések | 220 |
| Korreláció- és regresszió analizis | 223 |
| Valószinüségi változók közötti sztochasztikus kapcsolatokról | 223 |
| Regressziós-görbék. Feltételes várható érték és feltételes szórásnégyzet | 225 |
| Regresszió a legkisebb négyzetek elve alapján. Kétváltozós normális eloszlás esete | 227 |
| Lineáris regresszió | 229 |
| Korreláció és regresszió több változó eseteén | 235 |
| Parciális-korreláció | 239 |
| Táblázatok | 243 |
| Irodalomjegyzék | 255 |
Témakörök
Dr. Reimann József
Dr. Reimann József műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Dr. Reimann József könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.