Valószínűségszámítás és matematikai statisztika

Szerző

Szelezsán János

Lektor

Dr. Arató Mátyás

Budapest

'Szelezsán János: Valószínűségszámítás és matematikai statisztika ' összes példány

Kiadó:	LSI Oktatóközpont
Kiadás helye:	Budapest
Kiadás éve:	1999
Kötés típusa:	Ragasztott papírkötés
Oldalszám:	315 oldal
Sorozatcím:
Kötetszám:
Nyelv:	Magyar
Méret:	24 cm x 17 cm
ISBN:	963-577-247-5
Megjegyzés:	Fekete-fehér ábrákkal illusztrálva.

Értesítőt kérek a kiadóról

A beállítást mentettük,
naponta értesítjük a beérkező friss
kiadványokról

Tartalom

Valószínűségszámítás
Események, tulajdonságok	11
Bevezetés	11
A valószínűségszámítás tárgya	11
Egy kis történeti áttekintés	13
Események és tulajdonságaik. Az eseménytér	14
Kísérlet, elemi események, speciális események	14
Elemi események	15
Eseménytér	16
Összetett események	16
Biztos esemény, lehetetlen esemény	16
Az események mint halmazok	17
Műveletek eseményekkel	18
Az ellentett esemény	18
Események összege	19
Események szorzata	19
Események különbsége	19
A műveletek tulajdonságai	20
Teljes eseményrendszer	21
A fejezet összefoglalása	22
Feladatok	23
A valószínűségszámítás	30
A valószínűség fogalma	30
Gyakoriság, relatív gyakoriság	30
A valószínűség	32
Definíció a relatív gyakorisággal	32
A valószínűség axiomatikus definíciója	33
Az axiómák következményei (valószínűségszámítási tételek)	34
A kombinatórikus valószínűség (a klasszikus képlet)	37
Mintavétel	39
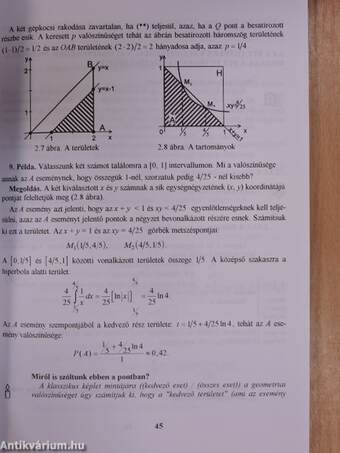
A geometriai valószínűség	42
A feltételes valószínűség. Valószínűségek meghatározása feltételes valószínűséggel	46
A feltételes valószínűség	46
A feltételes relatív gyakoriság	46
A feltételes valószínűség definíciója	47
A szorzási szabály	50
A teljes valószínűség tétele	51
A Bayes tétel	53
Események függetlensége	55
Független kísérletek	59
A fejezet összefoglalása	60
Felatatok	62
Valószínűségi változók, eloszlásaik és jellemzőik	71
A valószínűségi változó és eloszlása	71
A diszkrét valószínűségi változó és eloszlása	72
A diszkrét változó eloszlása	74
Folytonos valószínűségi változó és eloszlása	76
Az eloszlásfüggvény	77
Az eloszlásfüggvény tulajdonságai	81
Diszkrét eloszlások eloszlásfüggvénye	84
A sűrűségfüggvény	85
Valószínűségi változók függetlensége	91
Műveletek független valószínűségi változókkal. Változók függvényei	91
Műveletek	92
Transzformált eloszlások	94
A valószínűségi eloszlások jellemzői	97
A várható érték	97
Diszkrét valószínűségi változó várható értéke	98
Folytonos valószínűségi változó várható értéke	100
A várható érték tulajdonságai	102
A szórás	104
Diszkrét valószínűségi változó szórása	105
Folytonos valószínűségi változó szórása	106
A szórás tulajdonságai	107
A fejezet összefoglalása	110
Feladatok	112
Nevezetes eloszlások	121
Diszkrét eloszlások	121
A karakterisztikus eloszlás	121
Az egyenletes eloszlás	122
A binomiális eloszlás	123
A binomiális eloszlás egy interpretációja	124
A várható érték	124
A szórás	125
Hipergeometrikus eloszlás	127
A várható érték és a szórás	127
A binomiális és a hipergeometrikus eloszlás kapcsolata	128
A Poisson-eloszlás	129
A várható érték és a szórás	130
Folytonos eloszlások	133
Az egyenletes eloszlás	133
A várható érték	134
A szórás	134
Az exponenciális eloszlás	136
A normális eloszlás	140
Az eloszlásfüggvény	141
A várható érték	141
A szórás	142
A standard normális eloszlás	142
A normális eloszlásból származtatott fontos eloszlások	145
A fejezet összefoglalása	148
Feladatok	150
A nagy számok törvényei. A központi határeloszlás tétel	155
A nagy számok törvényei	155
A Markov tétel	155
A Csebisev-egyenlőtlenség	156
A nagy számok törvénye (Bernoulli tétel)	157
A várható érték és a számtani közép	160
A központi határeloszlás tétel	162
Egy fontos alkalmazás	163
A fejezet összefoglalása	165
Feladatok	165
Többdimenziós valószínűségeloszlások, valószínűségi vetkorváltozók és jellemzőik	168
Diszkrét valószínűségi vektorok	168
Együttes eloszlás	168
Peremeloszlás	169
Kétdimenziós folytonos eloszlások	172
Az együttes eloszlásfüggvény	173
Peremeloszlások	174
Diszkrét eloszlás eloszlásfüggvénye	174
Az esemény valószínűsége	175
Együttes sűrűségfüggvény	177
Perem-sűrűségfüggvények	179
Feltételes eloszlások	180
Diszkrét feltételes eloszlások	180
Folytonos feltételes eloszlások	182
A sűrűségfüggvény	182
Az eloszlásfüggvény	183
Valószínűségi változók függetlensége	184
Függetlenség diszkrét változókra	184
Függetlenség folytonos változókra	185
Együttes eloszlás várható értéke	187
Valószínűségi változók függvényeinek várható értéke	187
A diszkrét eloszlás esete	187
A folytonos eloszlás esete	188
A peremeloszlások várható értéke	189
A diszkrét változó esete	189
A folytonos eset	190
Valószínűségi változók összegének várható értéke	191
Valószínűségi változók szorzatának várható értéke	192
Nem független változók esetén	192
Független változók esetén	192
Feltételes eloszlások várható értéke	193
A diszkrét eset	193
A folytonos eset	195
A korrelációs együttható	195
A kovariancia	197
A kovariancia diszkrét esetre	198
A kovariancia folytonos esetre	198
A korrelációs együttható	198
Regresszióanalízis	202
A regressziós függvény	203
A regressziós függvény diszkrét esetben	203
A regressziós függvény folytonos változókra	204
A regressziós függvény mint jó közelítés	205
Másodfajú regresszió	207
Lineráris regresszió	207
n-dimenziós eloszlások	209
Néhány nevezetes többdimenciós eloszlás	210
Diszkrét eloszlások	210
Folytonos eloszlások	210
A fejezet összefoglalása	211
Feladatok	215
Matematikai statisztika
Statisztikai minták és jellemzőik	223
Statisztikai sokaság, mintavétel	224
A statisztikai következtetésről	225
A minta vizsgálata osztályközök segítségével	226
A minta statisztika jellemzői	227
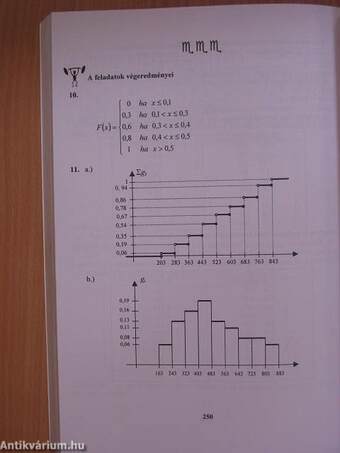
A tapasztalati (empirikus) eloszlásfüggvény	228
A közelítő tapasztalati eloszlásfüggvény	230
Hisztogramok	232
Gyakorisági hisztogram	232
Sűrűséghisztogram	233
A tapasztalati (empirikus) várható érték. A mintaközép	234
Empirikus szórásnégyzet	236
Korrigált empirikus szórásnégyzet	238
A szórás csoportosított minta esetén	239
A szórás osztályközökkel adott minta esetén	240
A tapasztalati medián	241
Középeltérés vagy átlagos eltérés	241
A fejezet összefoglalása	242
Feladatok	243
Statisztikai becslések	253
Pontbecslések	254
A statisztikai függvény. Jó tulajdonságú becslések	254
A maximum likelihood módszer statisztikai becslések konstrukciójára	256
Becslés exponenciális eloszlás várható értékére	257
Normális eloszlás várható értékének és szórásának a becslése	258
A becslés a Poisson-eloszlásnál	259
Becslés a P(A) valószínűségre	260
Intervallumbecslés. Megbízhatósági (konfidencia) intervallumok	261
A várható érték becslése ismert szórás esetén	262
Konfidencia intervallum normális eloszlású változó várható értékére ismeretlen szórás esetén	266
Normális eloszlás szórásának becslése	268
Konfidenciaintervallum ismeretlen valószínűségre	270
A fejezet összefoglalása	271
Feladatok	273
Statisztikai hipotézisek vizsgálata	276
A statisztikai próba	277
A statisztikai próba fogalma. Hipotézishibák	277
Nevezetes statisztikai próbák	280
Paraméteres próbák	281
Az egymintás u-próba. Hipotézis a várható értékre, ismert szórás mellett	281
Kétmintás u-próba. Hipotézis a várható értékek egyezőségére	284
Egymintás t-próba. Hipotézis a várható értékre ismeretlen szórás esetén	285
Kétmintás t-próba. Hipotézis a várható értékek egyenlőségére	286
Az F-próba. Hipotézis a szórások egyezőségére	288
Nemparaméteres próbák	290
Illeszkedésvizsgálat	291
Becslés illeszkedésvizsgálat. Homogenitásvizsgálat	294
A fejezet összefoglalása	296
Feladatok	298
A korrelációs együttható és a regressziós egyenes statisztikai becslése	302
Az "empirikus" korrrelációs együttható	302
A regressziós egyenes	303
A statisztikai módszer	304
A legkisebb négyzetek módszere	305
A fejezet összefoglalása	308
Feladatok	309
Irodalomjegyzék	311
Függelék
A. táblázat	312
B. táblázat	313
C. táblázat	314
D. táblázat	315

Témakörök

Szelezsán János

Szelezsán János műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: Szelezsán János könyvek, művek

Megvásárolható példányok

Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.

Előjegyzem